Algorithm

Problem Name: 840. Magic Squares In Grid

Problem Link: https://leetcode.com/problems/magic-squares-in-grid/
 

A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.

Given a row x col grid of integers, how many 3 x 3 "magic square" subgrids are there?  (Each subgrid is contiguous).

 

Example 1:

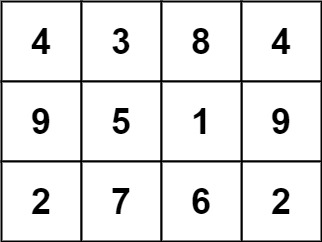
Input: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]]
Output: 1
Explanation: 
The following subgrid is a 3 x 3 magic square:

while this one is not:

In total, there is only one magic square inside the given grid.

Example 2:

Input: grid = [[8]]
Output: 0

 

Constraints:

  • row == grid.length
  • col == grid[i].length
  • 1 <= row, col <= 10
  • 0 <= grid[i][j] <= 15

Code Examples

#1 Code Example with Python Programming

Code - Python Programming


class Solution:
    def numMagicSquaresInside(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        res = 0
        for i in range(len(grid)-2):
            for j in range(len(grid)-2):
                if sum(grid[i][j: j + 3]) == sum(grid[i + 1][j : j +3]) == sum(grid[i + 2][j:j + 3]) == sum(grid[k][j] for k in range(i, i + 3)) == sum(grid[k][j + 1] for k in range(i, i + 3)) == sum(grid[k][j + 2] for k in range(i, i + 3)) == (grid[i][j] + grid[i + 1][j + 1] + grid[i + 2][j + 2]) == (grid[i+2][j]+ grid[i + 1][j + 1] + grid[i][j + 2]): 
                    if set(grid[i][j: j + 3] + grid[i + 1][j: j +3] + grid[i + 2][j:j + 3]) == {1,2,3,4,5,6,7,8,9}: res += 1
        return res
Copy The Code & Try With Live Editor

Input

x
–
+
cmd
grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]]

Output

x
–
+
cmd
1

#2 Code Example with C# Programming

Code - C# Programming


namespace LeetCode
{
    public class _0840_MagicSquaresInGrid
    {
        public int NumMagicSquaresInside(int[][] grid)
        {
            int rows = grid.Length, cols = grid[0].Length;
            int ans = 0;
            for (int r = 1; r  <  rows - 1; r++)
                for (int c = 1; c  <  cols - 1; c++)
                {
                    if (grid[r][c] != 5) continue;
                    if (IsMagic(new int[] { grid[r - 1][c - 1], grid[r - 1][c],     grid[r - 1][c + 1],
                                            grid[r][c - 1],     grid[r][c],         grid[r][c + 1],
                                            grid[r + 1][c - 1], grid[r + 1][c],     grid[r + 1][c + 1] }))
                        ans++;
                }

            return ans;
        }

        private bool IsMagic(int[] arr)
        {
            var count = new int[16];
            foreach (int val in arr)
                count[val]++;

            for (int i = 1; i  < = 9; i++)
                if (count[i] != 1)
                    return false;

            return (arr[0] + arr[1] + arr[2] == 15 &&
                    arr[3] + arr[4] + arr[5] == 15 &&
                    arr[6] + arr[7] + arr[8] == 15 &&
                    arr[0] + arr[3] + arr[6] == 15 &&
                    arr[1] + arr[4] + arr[7] == 15 &&
                    arr[2] + arr[5] + arr[8] == 15 &&
                    arr[0] + arr[4] + arr[8] == 15 &&
                    arr[2] + arr[4] + arr[6] == 15);
        }
    }
}
Copy The Code & Try With Live Editor

Input

x
–
+
cmd
grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]]

Output

x
–
+
cmd
1
Advertisements

Demonstration

Previous
#479 Leetcode Largest Palindrome Product Solution in C, C++, Java, JavaScript, Python, C# Leetcode