Algorithm
problem link- https://www.spoj.com/problems/LCA/
LCA - Lowest Common Ancestor
A tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree. - Wikipedia
The lowest common ancestor (LCA) is a concept in graph theory and computer science. Let T be a rooted tree with N nodes. The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants (where we allow a node to be a descendant of itself). - Wikipedia
Your task in this problem is to find the LCA of any two given nodes v and w in a given tree T.
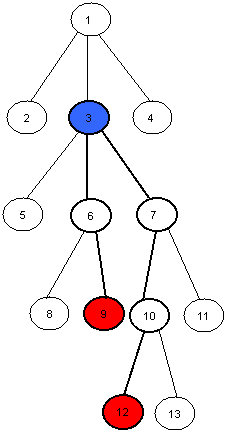
For example the LCA of nodes 9 and 12 in this tree is the node number 3.
Input
The first line of input will be the number of test cases. Each test case will start with a number N the number of nodes in the tree, 1 <= N <= 1,000. Nodes are numbered from 1 to N. The next N lines each one will start with a number M the number of child nodes of the Nth node, 0 <= M <= 999 followed by M numbers the child nodes of the Nth node. The next line will be a number Q the number of queries you have to answer for the given tree T, 1 <= Q <= 1000. The next Q lines each one will have two number v and w in which you have to find the LCA of v and w in T, 1 <= v, w <= 1,000.
Input will guarantee that there is only one root and no cycles.
Output
For each test case print Q + 1 lines, The first line will have “Case C:” without quotes where C is the case number starting with 1. The next Q lines should be the LCA of the given v and w respectively.
Example
Input: 1 7 3 2 3 4 0 3 5 6 7 0 0 0 0 2 5 7 2 7 Output: Case 1: 3 1
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define MOD 1000000007LL
#define EPS 1e-9
#define io ios_base::sync_with_stdio(false);cin.tie(NULL);
#define M_PI 3.14159265358979323846
template <typename T> T gcd(T a, T b){return (b==0)?a:gcd(b,a%b);}
template <typename T> T lcm(T a, T b){return a*(b/gcd(a,b));}
template <typename T> T mod_exp(T b, T p, T m){T x = 1;while(p){if(p&1)x=(x*b)%m;b=(b*b)%m;p=p>>1;}return x;}
template <typename T> T invFermat(T a, T p){return mod_exp(a, p-2, p);}
template <typename T> T exp(T b, T p){T x = 1;while(p){if(p&1)x=(x*b);b=(b*b);p=p>>1;}return x;}
const int MAXN = 1e3+5;
const int LG = log2(MAXN) + 1;
int n;
vector<int> adj[MAXN];
int level[MAXN], par[MAXN][LG];
void dfs(int u, int parent){
level[u] = level[parent] + 1;
par[u][0] = parent;
for(auto v : adj[u]){
if(v == parent) continue;
dfs(v, u);
}
}
int lca(int u, int v){
if(level[u] < level[v]) swap(u, v);
int log = log2(level[u]);
for(int i = log; i >= 0; i--)
if(level[u]-level[v] >= (1 << i))
u = par[u][i];
if(u == v)
return u;
for(int i = log; i >= 0; i--){
if(par[u][i] != -1 && par[u][i] != par[v][i]){
u = par[u][i];
v = par[v][i];
}
}
return par[u][0];
}
int main(){
io;
int tc = 1;
int t;
cin >> t;
while(t--){
cout << "Case " << tc << ":" << endl;
tc++;
cin >> n;
for(int i = 1;i <= n; i++){
adj[i].clear();
level[i] = 0;
}
for(int i = 1;i <= n; i++){
int children;
cin >> children;
for(int j = 0;j < children; j++){
int a;
cin >> a;
adj[i].push_back(a);
adj[a].push_back(i);
}
}
memset(par, -1, sizeof par);
level[0] = -1;
dfs(1, 0);
for(int j = 1; j < LG; j++){
for(int i = 1; i <= n; i++){
if(par[i][j-1] != -1)
par[i][j] = par[par[i][j-1]][j-1];
}
}
int q;
cin >> q;
while(q--){
int a, b;
cin >> a >> b;
cout << lca(a, b) << endl;
}
}
return 0;
}Input
7
3 2 3 4
0
3 5 6 7
0
0
0
0
2
5 7
2 7
Output
3
1
Demonstration
SPOJ Solution-Lowest Common Ancestor-Solution in C, C++, Java, Python