Algorithm
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <cstdio>
#include <vector>
#include <set>
int main(){
int n(0), m(0); scanf("%d %d", &n, &m);
std::vector<int> degree(n + 1,0);
std::set<std::pair<int, int>> edges;
for(int k = 0; k < m; k++){
int left(0), right(0); scanf("%d %d", &left, &right);
edges.insert(std::pair<int,int>(left,right));
++degree[left]; ++degree[right];
}
int numGroups(0);
while(edges.size() > 0){
std::vector<int> toDecrease;
for(int k = 0; k <= n; k++){
if(degree[k] == 1){
toDecrease.push_back(k);
std::set<std::pair<int,int>>::iterator setIter;
for(setIter = edges.begin(); setIter != edges.end(); setIter++){
if(setIter->first == k){toDecrease.push_back(setIter->second); edges.erase(setIter); break;}
else if(setIter->second == k){toDecrease.push_back(setIter->first); edges.erase(setIter); break;}
}
}
}
if(toDecrease.size() == 0){break;}
else{
for(int k = 0; k < toDecrease.size(); k++){--degree[toDecrease[k]];}
++numGroups;
}
}
printf("%d\n", numGroups);
return 0;
}Input
3 3
1 2
2 3
3 1
1 2
2 3
3 1
Demonstration
Codeforces Solution-B. Students and Shoelaces-Solution in C, C++, Java, Python

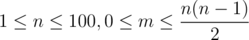 ). The students are numbered from
). The students are numbered from