Codeforces Solution-E. Cyclic Components-Solution in C, C++, Java, Python

Algorithm

You are given an undirected graph consisting of $n$ vertices and $m$ edges. Your task is to find the number of connected components which are cycles.

Here are some definitions of graph theory.

An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex $a$ is connected with a vertex $b$ , a vertex $b$ is also connected with a vertex $a$ ). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.

Two vertices $u$ and $v$ belong to the same connected component if and only if there is at least one path along edges connecting $u$ and $v$ .

A connected component is a cycle if and only if its vertices can be reordered in such a way that:

the first vertex is connected with the second vertex by an edge,
the second vertex is connected with the third vertex by an edge,
...
the last vertex is connected with the first vertex by an edge,
all the described edges of a cycle are distinct.

A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.

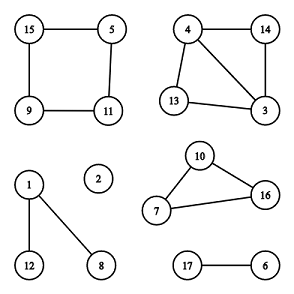$\text{[math]}$ There are

6

connected components,

2

of them are cycles:

[7, 10, 16]

and

[5, 11, 9, 15]

Input

The first line contains two integer numbers $n$ and $m$ ( $1 \leq n \leq 2 \cdot 10^{5}$ , $0 \leq m \leq 2 \cdot 10^{5}$ ) — number of vertices and edges.

The following $m$ lines contains edges: edge $i$ is given as a pair of vertices $v_{i}$ , $u_{i}$ ( $1 \leq v_{i}, u_{i} \leq n$ , $u_{i} \neq v_{i}$ ). There is no multiple edges in the given graph, i.e. for each pair ( $v_{i}, u_{i}$ ) there no other pairs ( $v_{i}, u_{i}$ ) and ( $u_{i}, v_{i}$ ) in the list of edges.

Output

Print one integer — the number of connected components which are also cycles.

Examples
input
Copy
5 4
1 2
3 4
5 4
3 5
output
Copy
1
input
Copy
17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6
output
Copy
2

Note

In the first example only component $[3, 4, 5]$ is also a cycle.

The illustration above corresponds to the second example.

Code Examples

#1 Code Example with C++ Programming

Code - C++ Programming

#include <bits/stdc++.h>

using namespace std;

int const N = 2e5 + 1;
int n, m, res;
bool vis[N];
vector<vector<int> > g;
vector<int> all;

void DFS(int u) {
  vis[u] = true;
  all.push_back(u);

  for(int i = 0;i < g[u].size(); ++i)
    if(!vis[g[u][i]])
      DFS(g[u][i]);
}

int main() {
  cin >> n >> m;
  g.resize(n);
  for(int i = 0, a, b; i < m; ++i) {
    cin >> a >> b;
    --a, --b;
    g[a].push_back(b);
    swap(a, b);
    g[a].push_back(b);
  }

  for(int i = 0; i < n; ++i) {
    if(!vis[i]) {
      all.clear();
      DFS(i);

      bool ok = true;
      for(int j = 0; j < all.size(); ++j)
        if(g[all[j]].size() != 2) {
          ok = false;
          break;
        }

      res += (ok && all.size() > 2);
    }
  }

  cout << res << endl;

  return 0;
}

Copy The Code & Try With Live Editor

Input

–

cmd

5 4
1 2
3 4
5 4
3 5

Output

–

cmd

Demonstration

Codeforces Solution-E. Cyclic Components-Solution in C, C++, Java, Python

Previous
Codeforces solution 1080-B-B. Margarite and the best present codeforces solution

Next
CodeChef solution DETSCORE - Determine the Score CodeChef solution C,C+

Try With Live Editor

Category - Codeforces Online Judge Maniruzzaman Akash 1 year ago 332 0