Algorithm
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <bits/stdc++.h>
using namespace std;
int const N = 1e5 + 1;
int n, m, a[N];
int main() {
scanf("%d %d", &n, &m);
long long Pow = 1;
while(n != 0 && Pow <= m) {
Pow *= 2;
--n;
}
if(n != 0) {
cout << m << endl;
} else {
cout << m % Pow << endl;
}
return 0;
}Input
4
42
42
Output
10
Demonstration
Codeforces Solution-Modular Exponentiation-Solution in C, C++, Java, Python

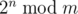 ,
,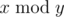 denotes the remainder of division of
denotes the remainder of division of 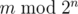 .
.