Algorithm
ZS the Coder and Chris the Baboon has explored Udayland for quite some time. They realize that it consists of n towns numbered from 1 to n.
There are n directed roads in the Udayland. i-th of them goes from town i to some other town ai (ai ≠ i). ZS the Coder can flip the direction of any road in Udayland, i.e. if it goes from town A to town B before the flip, it will go from town B to town A after.
ZS the Coder considers the roads in the Udayland confusing, if there is a sequence of distinct towns A1, A2, ..., Ak (k > 1) such that for every 1 ≤ i < k there is a road from town Ai to town Ai + 1 and another road from town Ak to town A1. In other words, the roads are confusing if some of them form a directed cycle of some towns.
Now ZS the Coder wonders how many sets of roads (there are 2n variants) in initial configuration can he choose to flip such that after flipping each road in the set exactly once, the resulting network will not be confusing.
Note that it is allowed that after the flipping there are more than one directed road from some town and possibly some towns with no roads leading out of it, or multiple roads between any pair of cities.
The first line of the input contains single integer n (2 ≤ n ≤ 2·105) — the number of towns in Udayland.
The next line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n, ai ≠ i), ai denotes a road going from town i to town ai.
Print a single integer — the number of ways to flip some set of the roads so that the resulting whole set of all roads is not confusing. Since this number may be too large, print the answer modulo 109 + 7.
3
2 3 1
6
4
2 1 1 1
8
5
2 4 2 5 3
28
Consider the first sample case. There are 3 towns and 3 roads. The towns are numbered from 1 to 3 and the roads are 
, 
, 
initially. Number the roads 1 to 3 in this order.
The sets of roads that ZS the Coder can flip (to make them not confusing) are {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}. Note that the empty set is invalid because if no roads are flipped, then towns 1, 2, 3 is form a directed cycle, so it is confusing. Similarly, flipping all roads is confusing too. Thus, there are a total of 6 possible sets ZS the Coder can flip.
The sample image shows all possible ways of orienting the roads from the first sample such that the network is not confusing.
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <bits/stdc++.h>
using namespace std;
int const N = 2e5 + 1, M = 1e9 + 7;
int n, low[N], idx[N], comp[N], sol[N], dfs, id;
bool in[N];
vector<int> st;
vector<vector<int> > g;
void DFS(int v) {
low[v] = idx[v] = dfs++;
in[v] = true;
st.push_back(v);
for(int i = 0; i < g[v].size(); i++)
if(idx[g[v][i]] == -1) {
DFS(g[v][i]);
low[v] = min(low[v], low[g[v][i]]);
} else if(in[g[v][i]])
low[v] = min(low[v], low[g[v][i]]);
if(low[v] == idx[v]) {
int node;
do {
node = st.back();
in[node] = false;
st.pop_back();
++comp[id];
} while(node != v);
id++;
}
}
int fst(int base, int power) {
int ret = 1;
while(power > 0) {
if(power % 2 == 0) {
power /= 2;
base = 1ll * base * base % M;
} else {
--power;
ret = 1ll * ret * base % M;
power /= 2;
base = 1ll * base * base % M;
}
}
return ret;
}
int main() {
cin >> n;
g.resize(n);
for(int i = 0; i < n; ++i) {
int tmp;
cin >> tmp;
g[i].push_back(--tmp);
}
memset(idx, -1, sizeof idx);
for(int i = 0; i < n; ++i)
if(idx[i] == -1)
DFS(i);
for(int i = 0; i < id; ++i)
sol[i] = (fst(2, comp[i]) - (comp[i] == 1 ? 0 : 2) + M) % M;
long long res = 1;
for(int i = 0; i < id; ++i)
res = res * sol[i] % M;
cout << res << endl;
return 0;
}Input
2 3 1
Output
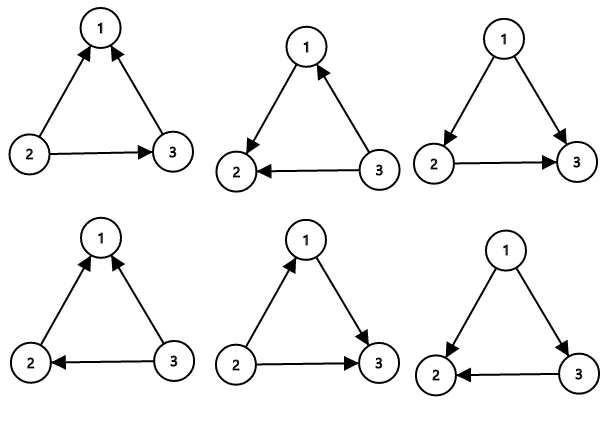
Demonstration
Codeforces Solution-Directed Roads-Solution in C, C++, Java, Python