Algorithm
In this problem we consider a very simplified model of Barcelona city.
Barcelona can be represented as a plane with streets of kind x=c and y=c for every integer c (that is, the rectangular grid). However, there is a detail which makes Barcelona different from Manhattan. There is an avenue called Avinguda Diagonal which can be represented as a the set of points (x,y) for which ax+by+c=0.
One can walk along streets, including the avenue. You are given two integer points A and B somewhere in Barcelona. Find the minimal possible distance one needs to travel to get to B from A.
The first line contains three integers a, b and c (−109≤a,b,c≤109, at least one of a and b is not zero) representing the Diagonal Avenue.
The next line contains four integers x1, y1, x2 and y2 (−109≤x1,y1,x2,y2≤109) denoting the points A=(x1,y1) and B=(x2,y2).
Find the minimum possible travel distance between A and B. Your answer is considered correct if its absolute or relative error does not exceed 10−6.
Formally, let your answer be a, and the jury's answer be b. Your answer is accepted if and only if |a−b|max(1,|b|)≤10−6.
1 1 -3 0 3 3 0
4.2426406871
3 1 -9 0 3 3 -1
6.1622776602
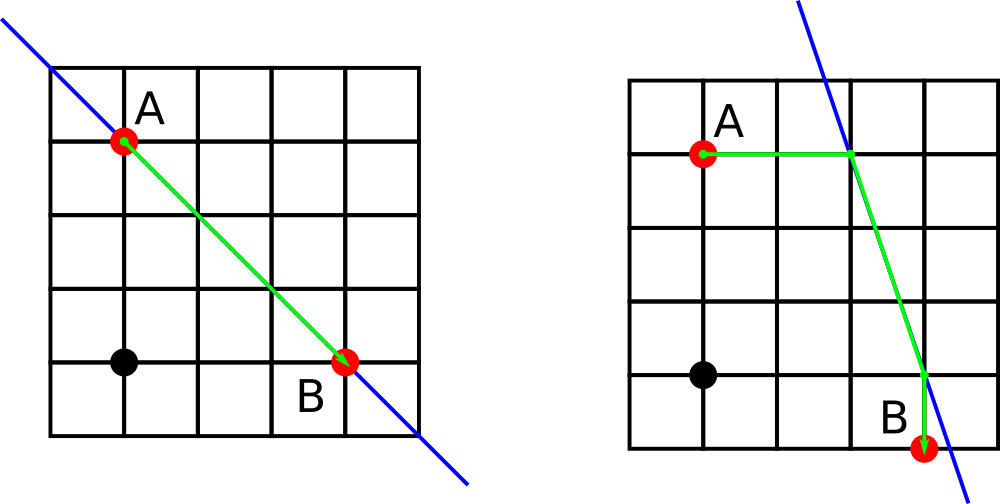
The first example is shown on the left picture while the second example us shown on the right picture below. The avenue is shown with blue, the origin is shown with the black dot.
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <bits/stdc++.h>
using namespace std;
struct line {
line() {}
line(double a, double b, double c) : a(a), b(b), c(c) {}
double a, b, c;
void print() {
printf("Line %lf %lf %lf\n", a, b, c);
}
};
struct point {
point() {}
point(double x, double y) : x(x), y(y) {}
double x, y;
bool ok() {
return x != FLT_MAX && y != FLT_MAX;
}
void print() {
printf("%lf %lf\n", x, y);
}
};
double dist(point a, point b) {
return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
line pointsToLine(point p1, point p2) {
if(fabs(p1.x - p2.x) < 1e-15)
return line(1.0, 0.0, -p1.x);
else {
line l;
l.a = -(double)(p1.y - p2.y) / (p1.x - p2.x);
l.b = 1.0;
l.c = -(double)(l.a * p1.x) - p1.y;
return l;
}
}
point lineLineIntersection(line l1, line l2) {
double det = l1.a * l2.b - l2.a * l1.b;
if(det == 0)
return point(FLT_MAX, FLT_MAX);
else {
double x = (l1.b * l2.c - l2.b * l1.c) / det;
double y = (l2.a * l1.c - l1.a * l2.c) / det;
return point(x, y);
}
}
line l;
point p, q;
int main() {
scanf("%lf %lf %lf", &l.a, &l.b, &l.c);
scanf("%lf %lf %lf %lf", &p.x, &p.y, &q.x, &q.y);
line lp1 = pointsToLine(p, point(p.x, p.y + 1.0));
line lp2 = pointsToLine(p, point(p.x + 1.0, p.y));
line lq1 = pointsToLine(q, point(q.x, q.y + 1.0));
line lq2 = pointsToLine(q, point(q.x + 1.0, q.y));
point ps1 = lineLineIntersection(l, lp1);
point ps2 = lineLineIntersection(l, lp2);
point qs1 = lineLineIntersection(l, lq1);
point qs2 = lineLineIntersection(l, lq2);
double res = 2e18;
if(ps1.ok() && qs1.ok())
res = min(res, dist(p, ps1) + dist(ps1, qs1) + dist(qs1, q));
if(ps1.ok() && qs2.ok())
res = min(res, dist(p, ps1) + dist(ps1, qs2) + dist(qs2, q));
if(ps2.ok() && qs1.ok())
res = min(res, dist(p, ps2) + dist(ps2, qs1) + dist(qs1, q));
if(ps2.ok() && qs2.ok())
res = min(res, dist(p, ps2) + dist(ps2, qs2) + dist(qs2, q));
printf("%.10lf\n", min(res, fabs(p.x - q.x) + fabs(p.y - q.y)));
return 0;
}Input
0 3 3 0
Output
Demonstration
Codeforces Solution-D. Barcelonian Distance-Solution in C, C++, Java, Python,Barcelonian Distance,Codeforces Solution
