Algorithm

B. Han Solo and Lazer Gun
time limit per test
1 second
memory limit per test
256 megabytes
problem link- https://codeforces.com/problemset/problem/514/B
input
standard input
output
standard output

There are n Imperial stormtroopers on the field. The battle field is a plane with Cartesian coordinate system. Each stormtrooper is associated with his coordinates (x, y) on this plane.

Han Solo has the newest duplex lazer gun to fight these stormtroopers. It is situated at the point (x0, y0). In one shot it can can destroy all the stormtroopers, situated on some line that crosses point (x0, y0).

Your task is to determine what minimum number of shots Han Solo needs to defeat all the stormtroopers.

The gun is the newest invention, it shoots very quickly and even after a very large number of shots the stormtroopers don't have enough time to realize what's happening and change their location.

Input

The first line contains three integers n, x0 и y0 (1 ≤ n ≤ 1000,  - 104 ≤ x0, y0 ≤ 104) — the number of stormtroopers on the battle field and the coordinates of your gun.

Next n lines contain two integers each xi, yi ( - 104 ≤ xi, yi ≤ 104) — the coordinates of the stormtroopers on the battlefield. It is guaranteed that no stormtrooper stands at the same point with the gun. Multiple stormtroopers can stand at the same point.

Output

Print a single integer — the minimum number of shots Han Solo needs to destroy all the stormtroopers.

Examples
input
Copy
4 0 0
1 1
2 2
2 0
-1 -1
output
Copy
2
input
Copy
2 1 2
1 1
1 0
output
Copy
1
Note

Explanation to the first and second samples from the statement, respectively:



 

Code Examples

#1 Code Example with C++ Programming

Code - C++ Programming

#include <bits/stdc++.h>

using namespace std;

int const N = 1e3 + 1;
int n, x, y, xx[N], yy[N];
bool vis[N];

bool collinear(int i, int j) {
  return fabs((y - yy[i]) * (x - xx[j]) - (y - yy[j]) * (x - xx[i])) <= 1e-9;
}

int main() {
  scanf("%d %d %d", &n, &x, &y);
  for(int i = 0; i < n; ++i)
    scanf("%d %d", xx + i, yy + i);
  
  int res = 0;

  for(int i = 0; i < n; ++i) {
    if(vis[i])
      continue;
    
    for(int j = 0; j < n; ++j) {
      if(vis[j])
        continue;
      
      if(collinear(i, j))
        vis[j] = true;
    }

    vis[i] = true;
    ++res;
  }

  printf("%d\n", res);

  return 0;
}
Copy The Code & Try With Live Editor

Input

x
–
+
cmd
4 0 0
1 1
2 2
2 0
-1 -1

Output

x
–
+
cmd
2
Advertisements

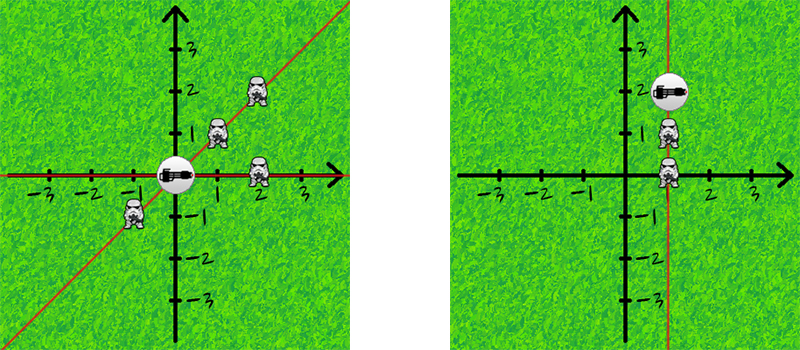
Demonstration

Codeforces Solution -Han Solo and Lazer Gun-Solution in C, C++, Java, Python

Previous
Codeforces solution 1080-B-B. Margarite and the best present codeforces solution
Next
CodeChef solution DETSCORE - Determine the Score CodeChef solution C,C+