Algorithm
Scrooge McDuck keeps his most treasured savings in a home safe with a combination lock. Each time he wants to put there the treasures that he's earned fair and square, he has to open the lock.

The combination lock is represented by n rotating disks with digits from 0 to 9 written on them. Scrooge McDuck has to turn some disks so that the combination of digits on the disks forms a secret combination. In one move, he can rotate one disk one digit forwards or backwards. In particular, in one move he can go from digit 0 to digit 9 and vice versa. What minimum number of actions does he need for that?
The first line contains a single integer n (1 ≤ n ≤ 1000) — the number of disks on the combination lock.
The second line contains a string of n digits — the original state of the disks.
The third line contains a string of n digits — Scrooge McDuck's combination that opens the lock.
Print a single integer — the minimum number of moves Scrooge McDuck needs to open the lock.
5
82195
64723
13
In the sample he needs 13 moves:
- 1 disk:
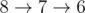
- 2 disk:
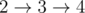
- 3 disk:
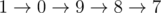
- 4 disk:

- 5 disk:
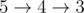
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
#define debug(n) cout<<(n)<<endl;
const ll INF = 2e18 + 99;
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n;
cin>>n;
string s, t;
cin>>s>>t;
int count = 0;
for(int i = 0; i < n; i++){
int a = s[i] - '0';
int b = t[i] - '0';
int g = min(a, b);
int h = max(a, b);
int c = min(h - g, (g + 10 - h));
count += c;
}
cout<<count<<endl;
}Input
82195
64723
Output
Demonstration
Codeforcess Solution 540-A A. Combination Lock ,C++, Java, Js and Python ,540-A,Codeforcess Solution
