Algorithm
DFSr - Depth Hierarchy
By Neilor Tonin, URI  Brazil
Brazil
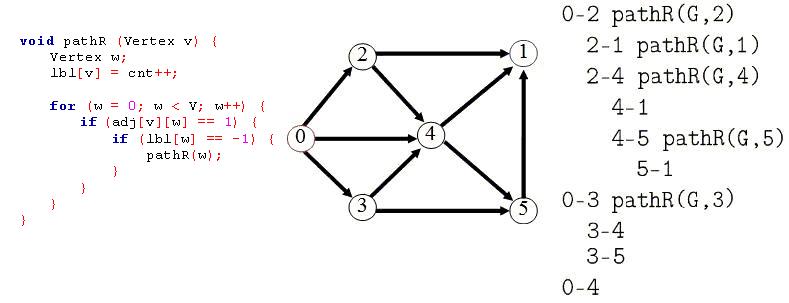
In graphs, the PathR function is well-known. It's called dfs or dfsr. It means a recursive deph-searching in nodes of a graph, using backtracking. The task here is, from an input graph, generate the hierarquie design of the searched nodes. To help you, is given the PathR procedure, listed above.
Input
The input file contains many test cases. The first line of the input file contains an integer N that represents the quantity of test cases that follows. Each one of N test cases contains, in the first line, two informations: (1 ≤ V ≤ 20) and E (1 ≤ E ≤ 20), that are respectively the amount of vertices and edges of the graph. Follow E lines containing informations over all of the edges of this graph.
Output
For each test case, an output must be printed that represents a depth search for all nodes, with respect of the hierarquie of each of them. The character b means a blank space. See the follewing example:
bb0-2 pathR(G,2)
bbbb2-1 pathR(G,1)
bbbb2-4 pathR(G,4)
bbbbbb4-1
And so on...
Obs.: The program should print a blank line after each test case, even after the last test case.
| Input Sample | Output Sample |
|
2 |
Caso 1: |
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define MAX 20
#define sc(a) scanf("%d", &a);
#define sc2(a, b) scanf("%d%d", &a, &b);
bool disc[MAX];
int graph[MAX][MAX];
void clean(int v) {
int i, j;
for (i = 0; i < v; i++) {
for (j = 0; j < v; j++)
graph[i][j] = 0;
disc[i] = false;
}
}
bool dfs(int v, int n, int s) {
int i;
bool path = false;
disc[v] = true;
for (i = 0; i < n; i++) {
if (graph[v][i] == 1) {
path = true;
if (!disc[i]) {
cout << string(s, ' ');
printf("%d-%d pathR(G,%d)n", v, i, i);
dfs(i, n, s + 2);
} else {
cout << string(s, ' ');
printf("%d-%dn", v, i);
}
}
}
return path;
}
void dfs_runner(int v) {
int i, ind = 0;
while (1) {
if (dfs(ind, v, 2))
puts("");
ind = -1;
for (i = 0; i < v; i++) {
if (!disc[i]) {
ind = i;
break;
}
}
if (ind == -1)
break;
}
}
int main(int argc, char const *argv[]) {
int n, v, e, o, d, c = 1;
sc(n);
while(n--) {
sc2(v, e);
clean(v);
while(e--) {
sc2(o, d);
graph[o][d] = 1;
}
printf("Caso %d:n", c++);
dfs_runner(v);
}
return 0;
}
Input
Output
