Algorithm
Problem Name: 2 AD-HOC - beecrowd | 2392
Problem Link: https://www.beecrowd.com.br/judge/en/problems/view/2392
Pulo do Sapo
Por OBI - Olimpíada Brasileira de Informática 2011  Brazil
Brazil
Timelimit: 1
Sebastião Bueno Coelho, apelidado de SBC pelos familiares e amigos, passou as férias de janeiro de 2011 no sítio de seus avós. Durante sua estadia, uma das atividades prediletas do SBC era nadar no rio que havia no fundo da casa onde morava.
Uma das características do rio que mais impressionava SBC era um belo caminho, feito inteiramente com pedras brancas. Há muito tempo, o avô de SBC notara que os habitantes do sítio atravessavam o rio com grande frequência e, por isso, construiu um caminho no rio com pedras posicionadas em linha reta; ao fazê-lo, tomou muito cuidado para que o espaçamento das pedras fosse de exatamente um metro.
Hoje em dia, a única utilidade do caminho é servir de diversão para os sapos que vivem no rio, que pulam de uma pedra a outra agitadamente. Um certo dia, enquanto descansava e nadava nas águas, SBC assistiu atentamente às acrobacias dos bichos e notou que cada sapo sempre pulava (zero, uma ou mais vezes) uma quantidade fixa de metros.
SBC sabe que você participa da OBI todos os anos e, chegando na escola, resolveu desafiar-te com o seguinte problema: Dado o número de pedras no rio, o número de sapos, a pedra inicial sobre a qual cada sapo está (cada pedra é identificada por sua posição na sequência de pedras) e a distância que cada sapo pula, determinar as posições onde pode existir um sapo depois que SBC chega no rio.
No primeiro caso de teste abaixo, SBC indicou a existência de 5 pedras no rio e 2 sapos. Os sapos estavam inicialmente nas pedras 3 e 4. SBC também lhe disse que o primeiro sapo da entrada sempre pula 2 metros, e o segundo sempre pula 4 metros. A figura a seguir ilustra as possíveis pedras que podem ser ocupadas pelos sapos quando eles começam a pular.
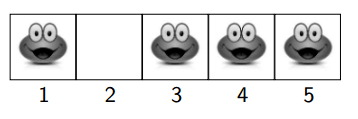
No segundo caso de teste abaixo, SBC indicou a existência de 8 pedras no rio e 3 sapos. Os sapos estavam inicialmente nas pedras 3, 2 e 6. SBC também lhe disse que o primeiro sapo da entrada sempre pula 3 metros, o segundo e terceiro sempre pulam 2 metros. Dessa forma, o primeiro sapo pode estar nas pedras 3 ou 6; o segundo sapo pode estar nas pedras 2, 4, 6 ou 8; e o terceiro sapo pode estar nas pedras 6, 4, 2 e 8. A figura a seguir ilustra as possíveis pedras que podem ser ocupadas pelos sapos quando eles começam a pular.

Entrada
A primeira linha da entrada contém dois inteiros N e M (1 ≤ N, M ≤ 100) representando o número de pedras no rio e o número de sapos, respectivamente. Cada uma das M linhas seguintes possui dois inteiros P e D (1 ≤ P, D ≤ N) representando a posição inicial de um sapo e a distância fixa de pulo, respectivamente.
Saída
A saída contém N linhas. A i-ésima linha indica a possibilidade ou não de ter um sapo na i-ésima pedra. Para as pedras que podem ter um sapo você deve imprimir 1, e para as pedras que com certeza não podem ter nenhum sapo você deve imprimir 0.
| Exemplos de Entrada | Exemplos de Saída |
|
5 2 3 2 4 4 |
1 0 1 1 1 |
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <cstdio>
int vetor[10000], n, sapos;
int main() {
scanf("%d %d", &n, &sapos);
for (int i = 0; i < sapos; i++) {
int inicial, distancia;
scanf("%d %d", &inicial, &distancia);
for (int k = inicial; k > 0; k -= distancia) vetor[k] = 1;
for (int k = inicial; k < = n; k += distancia) vetor[k] = 1;
}
for (int i = 1; i < = n; i++) printf("%d\n", vetor[i]);
return 0;
}
Input
3 2
4 4
Output
0
1
1
1
