Algorithm
Problem Name: beecrowd | 2769
Problem Link: https://www.beecrowd.com.br/judge/en/problems/view/2769
Assembly Line
By André Fillipi, INATEL  Brazil
Brazil
Timelimit: 1
With the spread of Industry 4.0's concepts and the development of Internet of Things, now it's simple to keep up with all the parts of a product's prodution in a assembly line. Having those informations, it is possible to optimize the production and reduce the time spent to have everything done.
An industry has the following production scheme:
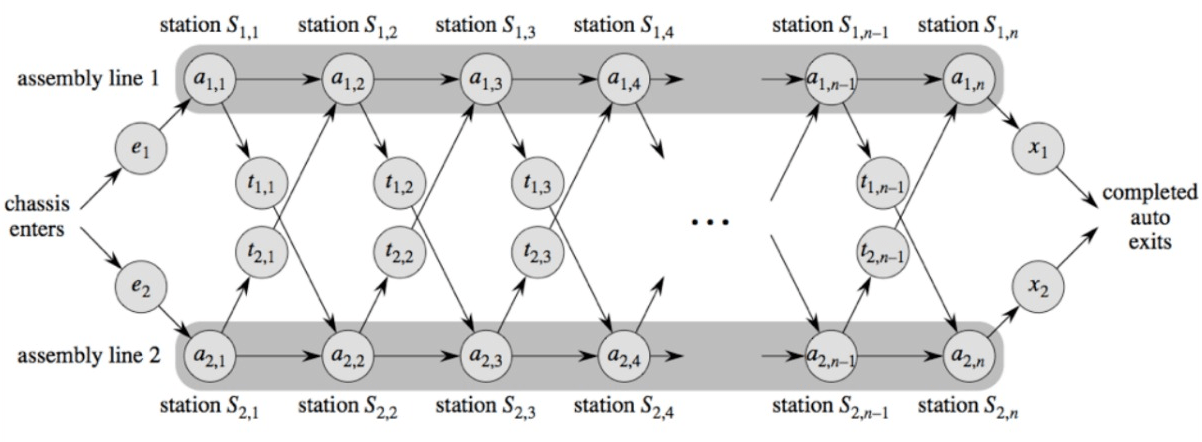
Knowing the time spent in each station, and the time required to swich between the assembly lines, calculate the least time spent to produce a single item.
Input
The input has multiples cases (EOF). The first line has an integer N, the number of steps of the production. The second line has two integers e1 and e2, the time spent to enter in each of the assembly lines. The next line has N values, a11, a12, ..., a1n, representing the time spent to execute the ith step on line 1. The next line has also N valores, a21, a22, ..., a2n representing the time spent to execute the ith step on line 2. The next two lines have N-1 integers representing the time to switch from line 1 to line 2, t11, t12, ..., t1n-1 and from line 2 to line 1, t21, t22, ..., t2n-1, respectively. Finally, two more integers x1 and x2 representing the time to exit from each assembly line.
Consider that number of steps per test case will be between 1 and 1000 and the other values between 0 and 105.
Output
The output shows the least time spent in the production.
| Input Sample | Output Sample |
|
3 1 1 1 2 3 3 2 1 1 2 2 1 1 1 |
7 |
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
#define MAX 1123
int N, a[2][MAX], t[2][MAX], e[2], x[2];
int pd[2][MAX];
int solve(int i, int j){
if(pd[i][j] != -1) return pd[i][j];
if(j == N) return pd[i][j] = a[i][j] + x[i];
if(j == 0) return pd[i][j] = e[i] + solve(i, j+1);
return pd[i][j] =
a[i][j] + min(solve(i, j+1), t[i][j] + solve(!i, j+1));
}
int main(){
int i, j;
while(scanf("%d", &N) != EOF){
scanf("%d %d", e, e+1);
for(i = 0; i < 2; i++)
for(j = 1; j < = N; j++)
scanf("%d", a[i]+j);
for(i = 0; i < 2; i++)
for(j = 1; j < N; j++)
scanf("%d", t[i]+j);
scanf("%d %d", x, x+1);
memset(pd, -1, sizeof(pd));
printf("%d\n", min(solve(0, 0), solve(1, 0))>;
}
return 0;
}
