Algorithm

Problem Name: beecrowd | 2161

Problem Link: https://www.beecrowd.com.br/judge/en/problems/view/2161

Square Root of 10

 

By M.C. Pinto, UNILA BR Brazil

Timelimit: 1

The method of periodic continued fractions is one of the many ways to calculate the square root of a natural number. This method uses as denominator a repetition for fractions. This repetition can be done by a fixed number of times.

For example, by repeating 2 times the continued fraction to calculate the square root of 10, we have the following equation.

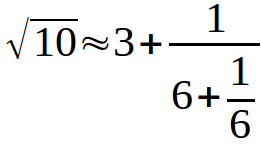
Your task is to calculate the approximate value of square root of 10 given the number N of repetitions.

 

Input

 

The input is a natural number N (0 ≤ N ≤ 100) that indicates the quantity of denominator repetitions in the continued fraction.

 

Output

 

The output is the approximate value of the square root with 10 decimal places.

 

 

 

Input Samples Output Samples

0

3.0000000000

 

 

 

1

3.1666666667

 

 

 

5

3.1622776623

 

Code Examples

#1 Code Example with C Programming

Code - C Programming


#include <stdio.h>

int main(void)
{
    int n;
    double ans=0.0;
    scanf("%i", &n);

    while(n)
    {
        ans+=6.0;
        ans=1.0/ans;
        --n;
    }
    ans+=3.0;

    printf("%.10lf\n", ans);
    return 0;
}
Copy The Code & Try With Live Editor

Output

x
–
+
cmd
3.0000000000

#2 Code Example with C++ Programming

Code - C++ Programming


#include <bits/stdc++.h>
using namespace std;

int main()
{
    int n;
    double calc = 0;
    cin >> n;
    while(n--){
        calc+=6;
        calc = 1/calc;
    }
    cout << fixed << setprecision(10) << 3+calc << endl;

    return 0;
}
Copy The Code & Try With Live Editor

Output

x
–
+
cmd
3.0000000000

#3 Code Example with Javascript Programming

Code - Javascript Programming

start coding...
Copy The Code & Try With Live Editor

Output

x
–
+
cmd
3.0000000000

#4 Code Example with Python Programming

Code - Python Programming


def r10(n):
    if n == 0:
        return 6
    x = 6+1/r10(n-1)
    return x

n = int(input())
x = r10(n)-3
print('%.10f' % x)
Copy The Code & Try With Live Editor

Output

x
–
+
cmd
3.0000000000
Advertisements

Demonstration

Previous
#2160 Beecrowd Online Judge Solution 2160 Name at Form Solution in C, C++, Java, Js and Python
Next
#2162 Beecrowd Online Judge Solution 2162 Peaks and Valleys Solution in C, C++, Java, Js and Python