Algorithm

Problem Name: 2 AD-HOC - beecrowd | 1472

Problem Link: https://www.beecrowd.com.br/judge/en/problems/view/1472

Triangles

 

Maratona de Programação da SBC Brasil

Timelimit: 1

It will be give to you N points on a circle. You must write a program to determine how many distinct equilateral triangles can be constructed using the given points as vertices.

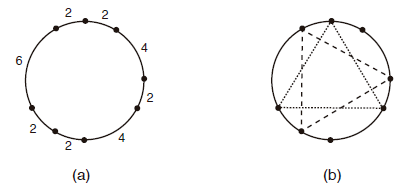
The figure below illustrates an example: (a) shows a set of points, determined by the lengths of the circular arcs that have adjacent points as extremes; and (b) shows the two triangles which can be built with these points.

 

Input

 

The input contains several test cases and ends with EOF. The first line of a test case contains an integer N ( 3 ≤ N ≤ 105), the number of points given. The second line contains N integers Xi (1 ≤ Xi ≤ 103) for 1 ≤ i ≤ N, representing the lengths of the circular arcs between two consecutive points in the circle: for 1 ≤ i ≤ (N − 1), Xi represents the length of the arc between points i and i + 1; XN represents the length of the arc between points N and 1.

 

Output

 

For each test case your program must output a single line, containing a single integer, the number of distinct equilateral triangles that can be constructed using the given points as vertices.

 

 

 

Sample Input Sample Output

8
4 2 4 2 2 6 2 2
6
3 4 2 1 5 3

2
1

 

Code Examples

#1 Code Example with C++ Programming

Code - C++ Programming


#include <bits/stdc++.h>

using namespace std;

int n;

int binarysearch(int v[], int chave)
{
	int inf = 0;
	int sup = n - 1;
	int meio;
	 
	while (inf  < = sup)
    {
        meio = inf + (sup-inf)/2;
        if (chave == v[meio])
            return meio;
        else if (chave  <  v[meio])
            sup = meio-1;
        else
            inf = meio+1;
    }
    return -1;
}

int main ()
{
	int ans[100010];
	
	int acc;
	int medida;
	
	int qtde;
	
	while(cin >> n)
	{
		acc = 0;
		qtde = 0;
		for (int i = 0; i  <  n; i++)
		{
			cin >> medida;
			acc+=medida;
			ans[i] = acc;
		}
		if (acc % 3 != 0) cout << "0\n";
		else
		{
			acc/=3;
			for (int i = 0 ; i  <  n; i++)
			{
				if (binarysearch(ans, ans[i]+acc) != -1)
					if (binarysearch(ans, ans[i]+2*acc) != -1) qtde++;
			}
			cout << qtde << '\n';
		}
	}
}
Copy The Code & Try With Live Editor

Input

x
–
+
cmd
8
4 2 4 2 2 6 2 2
6
3 4 2 1 5 3

Output

x
–
+
cmd
2
1
Advertisements

Demonstration

Previous
#1471 Beecrowd Online Judge Solution 1471 Dangerous Dive Solution in C, C++, Java, Js and Python
Next
#1478 Beecrowd Online Judge Solution 1478 Square Matrix II Solution in C++, Java, Js and Python