Algorithm
Problem Name: 2 AD-HOC - beecrowd | 2398
Problem Link: https://www.beecrowd.com.br/judge/en/problems/view/2398
Caça ao Tesouro
Por OBI - Olimpíada Brasileira de Informática 2011  Brazil
Brazil
Timelimit: 1
Capitão Tornado é um pirata muito cruel que faz qualquer coisa por dinheiro. Há alguns dias, o capitão soube da existência de um tesouro numa ilha deserta, e agora tenta determinar sua posição.
A ilha pode ser vista como um quadriculado N × N de terra cuja posição (0, 0) está a sudoeste, a posição (N−1, 0) está a sudeste, a posição (0, N−1) está a noroeste e a posição (N−1, N−1) está a nordeste. Em alguma posição desse quadriculado está o tesouro.
Uma curiosidade importante é a perna de pau que o capitão possui. Ela impede que o capitão se locomova em direções que não a horizontal ou a vertical: para ir da posição (1, 1) para a posição (3, 2), por exemplo, o capitão é obrigado a gastar três passos. É claro que o capitão sempre escolhe, dentro de suas limitações, um caminho com o menor número de passos possível. Chamamos esse modo de andar de passos de capitão. Um exemplo de caminho por passos de capitão entre (1, 1) e (3, 2) é ilustrado na figura a seguir.
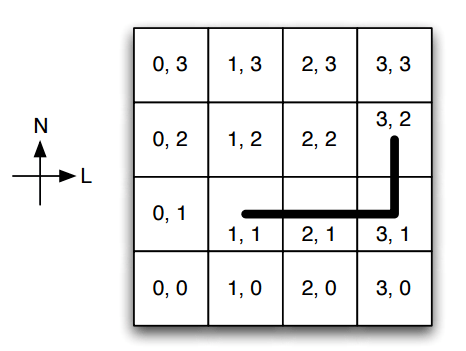
Como em toda boa caça ao tesouro, o capitão não conhece a posição onde o tesouro se encontra: ele possui um mapa que corresponde à geografia da ilha. Em algumas posições desse mapa, existem pistas escritas. Cada pista consiste em um número D, que indica a menor distância em passos de capitão entre a posição em que a pista se encontra e a do tesouro.
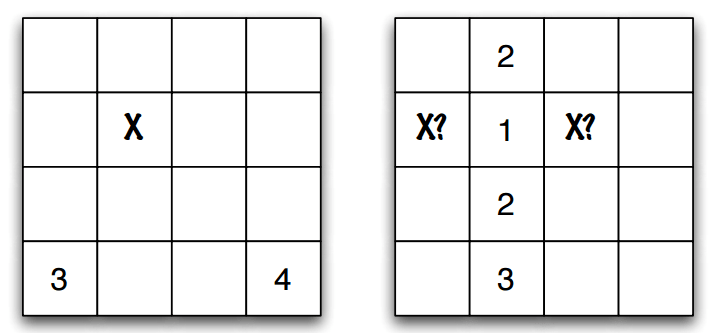
Observe que, dependendo da disposição das pistas, a posição do tesouro pode estar determinada de maneira única ou não. Na figura acima e à esquerda, as duas pistas são suficientes para se saber, com certeza, onde está o tesouro; na figura à direita, as quatro pistas dadas ainda possibilitam que tanto a posição (0, 2) quanto a (2, 2) guardem o tesouro. Nesse último caso, não se pode determinar, com certeza, qual é a localização do tesouro.
Dadas as pistas que o capitão possui, sua tarefa é determinar se as pistas fornecem a localização exata do tesouro e, caso positivo, qual ela é.
Entrada
A primeira linha contém dois inteiros positivos N (2 ≤ N ≤ 100) e K (1 ≤ K ≤ 100), onde N é a dimensão do quadriculado e K é o número de pistas no mapa que o capitão possui.
Cada uma das próximas K linhas contêm três inteiros X, Y e D, informando que existe uma pista na posição (X, Y) contendo o número D. Essa pista indica que o tesouro encontra-se a D passos de capitão da posição da pista.
É garantido que, com essas pistas, existe ao menos uma localização possível para o tesouro. Além disso, o mapa não contém duas pistas na mesma posição.
Saída
Se as pistas forem suficientes para determinar com certeza a localização do tesouro, seu programa deve imprimir uma única linha com dois inteiros, X e Y , indicando que o tesouro encontra-se na posição (X, Y).
Caso contrário, seu programa deve imprimir uma única linha com dois inteiros iguais a −1, como nos exemplos de saída a seguir.
| Exemplos de Entrada | Exemplos de Saída |
|
4 2 0 0 3 3 0 4 |
1 2 |
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <vector>
#define MAXN 110
using namespace std;
int main() {
int n, k, resposta = 0, resp1, resp2;
vector < pair<int, pair<int, int> > > pares;
scanf("%d %d", &n, &k);
for (int i = 0; i < k; i++) {
int x, y, z;
scanf("%d %d %d", &x, &y, &z);
pares.push_back(make_pair(z, make_pair(x, y)));
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
int pode_ser = 1;
for (int k = 0; k < pares.size(); k++) {
pair<int, pair<int, int> > par = pares[k];
if (abs(i - par.second.first) + abs(j - par.second.second) !=
par.first) {
pode_ser = 0;
break;
}
}
if (pode_ser) {
resp1 = i;
resp2 = j;
resposta++;
}
if (resposta > 1) {
printf("-1 -1\n");
return 0;
}
}
}
if (resposta == 1)
printf("%d %d\n", resp1, resp2);
else
printf("-1 -1\n");
return 0;
}
Input
0 0 3
3 0 4
Output
