Algorithm
Problem Name: 2 AD-HOC - beecrowd | 2323
Móbile
Por OBI - Olimpíada Brasileira de Informática 2007  Brazil
Brazil
Timelimit: 1
Móbiles são objetos muito populares hoje em dia, sendo encontrados até em berços, para diversão de bebês, mas foram concebidos há muito tempo (em 1931) pelo então jovem artista americano Alexander Calder como esculturas em movimento. Um móbile é uma estrutura composta de peças unidas por fios. O móbile é preso por um fio a uma argola pela qual ele é suspenso, permitindo que a estrutura movimente-se livremente. A argola é presa a uma única peça, chamada de peça-raiz do móbile. A peça-raiz pode ter zero ou mais sub-móbiles pendurados nela, cada sub-móbile sendo composto por uma peça-raiz na qual por sua vez podem estar pendurados zero ou mais sub-móbiles, e assim sucessivamente. Abaixo podemos ver dois exemplos de móbiles:
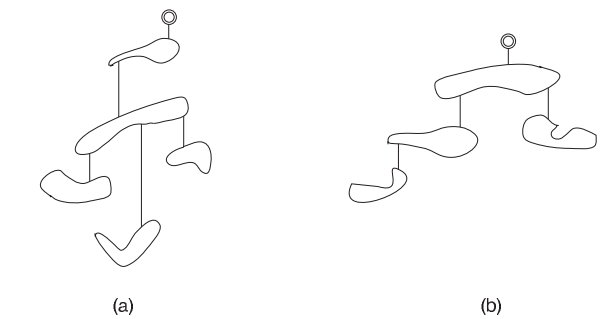
Victor é dono de uma fabrica de móbiles que emprega centenas de artesãos. Cada móbile produzido na fábrica é confeccionado por um artesão, que cria móbiles de acordo com o seu gosto pessoal, utilizando peças de formatos distintos. Entretanto, Victor tem notado que nem todos os seus artesãos possuem a mesma habilidade artística, de forma que às vezes o móbile produzido nem sempre é bem balanceado, segundo a sua concepção. Para Victor, um móbile é bem balanceado se, para cada peça, todos os sub-móbiles pendurados nela são compostos pelo mesmo número de peças. O número de peças de um sub-móbile é determinado contando-se o número de peças que o compõe, incluindo a sua peça-raiz. Note que cada peça do móbile, exceto a peça-raiz, é pendurada em exatamente uma outra peça.
Por exemplo, o móbile da figura (a) acima é um móbile bem balanceado: a peça-raiz possui um único sub-móbile, que por sua vez possui três sub-móbiles, todos com o mesmo número de peças (uma única). Já o móbile da figura (b) é um móbile mal balanceado: a peça-raiz possui dois sub-móbiles, um com o total de duas peças e outro com o total de uma peça.
Dada a descrição de um móbile, você deve escrever um programa para determinar se o móbile está bem balanceado ou não.
Entrada
A entrada contém um único conjunto de testes, que deve ser lido do dispositivo de entrada padrão (normalmente o teclado). A primeira linha da entrada contém um inteiro N que indica o número de peças utilizadas no móbile (1 ≤ N ≤ 10.000). As peças são identificadas por inteiros de 1 a N . Cada uma das N linhas seguintes contém dois números inteiros I e J , indicando que a peça de número I está pendurada na peça de número J (a peça raiz está pendurada na argola, que é identificada pelo o número 0).
Saída
Seu programa deve imprimir, na saída padrão, uma única linha, contendo a palavra bem se o móbile estiver bem balanceado ou mal caso esteja mal balanceado. A palavra deve ser escrita com todas as letras em minúsculas.
| Exemplos de Entrada | Exemplos de Saída |
|
3 |
bem |
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <cstdio>
#include <set>
#include <vector >
#define PB push_back
#define MAXN 10010
using namespace std;
bool condicional, visitado[MAXN];
vector<int> grafo[MAXN];
int dfs(int u) {
visitado[u] = true;
set < int> pesos;
int resposta = 1;
for (int i = 0; i < grafo[u].size(); i++) {
int v = grafo[u][i];
if (!visitado[v]) {
int variavel = dfs(v);
pesos.insert(variavel);
resposta += variavel;
}
}
if (pesos.size() > 1) condicional = true;
return resposta;
}
int main() {
int n;
scanf("%d", &n);
for (int i = 1; i < = n; i++) {
int u, v;
scanf("%d %d", &u, &v);
grafo[v].PB(u);
}
dfs(0);
if (condicional)
printf("mal\n");
else
printf("bem\n");
return 0;
}
Input
1 0
2 1
3 2
Output
