Algorithm
Problem Name: 2 AD-HOC - beecrowd | 1086
Problem Link: https://www.beecrowd.com.br/judge/en/problems/view/1086
The Club Ballroom
By Ricardo Anido  Brazil
Brazil
Timelimit: 1
The Tingua Social Club is building its new ballroom. The club members wish to have the floor covered with wood planks, as they consider this to be the best for dancing. A lumberyard from the region donated a large quantity of good quality wooden planks to be used in the ballroom. The donated planks have all the same width, but have different lengths.
The ballroom is a rectangle of dimensions N x M meters. The planks must be placed juxtaposed, so that no plank superposes another, and the whole floor must be covered. They must be aligned, lengthwise, to one of the sides of the ballroom, and all planks must be parallel. The club members do not want too many joints in the floor, and therefore if a plank is not long enough to cover the distance between two opposite sides of the ballroom, it can be joined to at most one other plank to complete the distance. Furthermore, the chief-carpenter has a great respect for all woods, and would rather not seeing any plank. Therefore, he wants to know if it is possible to cover the floor with the set of planks donated, observing the restrictions described; in case it is possible, the chief-carpenter wish knowing the smallest number of planks he can use.
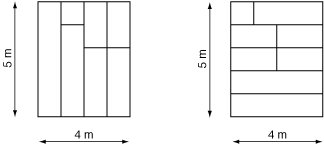
The figure below depicts two possible ways to cover the floor of a ballroom with dimensions 4 x 5 meters for a set of ten donated planks, with 100 cm width, and lengths 1, 2, 2, 2, 2, 3, 3, 4, 4 and 5 meters.
Input
The input contains several test cases. The first line of a test case contains two integers N and M indicating the dimensions, in meters, of the ballroom (1 ≤ N,M ≤ 104). The second line contains one integer L representing the planks width, in centimeters (1 ≤ L ≤ 100). The third line contains one integer K, indicating the number of planks donated (1 ≤ K ≤ 105). The fourth line contains K integers Xi, separated by spaces, representing the length, in meters, of one plank (1 ≤ Xi ≤ 104 for 1 ≤ i ≤ K). The end of input is indicated by a line containing only two zeros, separated by one space.
Output
For each one of the test cases in the input, your program must print one single line, containing one integer, the smallest number of planks needed to cover the whole floor, satisfying the restrictions established. If it is not possible to cover the whole floor satisfying the restrictions established, print one line with the word "impossivel" (which means impossible in Portuguese).
| Input Sample | Output Sample |
|
4 5 |
7 |
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
#include <bits/stdc++.h>
using namespace std;
#define min(a, b) (((a) < (b))?(a):(b))
#define max(a,b) (((a) > (b))?(a):(b))
int answer(int height, int planks_to_complete, vector <int>& planks) {
int begin, end, vertical_planks, planks_used;
begin = 0;
end = planks.size() - 1;
vertical_planks = 0;
planks_used = 0;
while (true) {
if (vertical_planks == planks_to_complete) break;
if (begin >= end) return 0;
if (planks[end] > height) end--;
else if (planks[end] == height) {
end--;
vertical_planks++;
planks_used++;
}
else {
if (begin != end) {
while (true) {
if (planks[begin] + planks[end] == height) {
begin++;
vertical_planks++;
planks_used += 2;
break;
}
if (planks[begin] + planks[end] > height)
break;
begin++;
}
end--;
}
}
}
return planks_used;
}
int main(){
int l1, l2, l, k;
int aws1, aws2;
while (true) {
cin >> l1 >> l2;
if ((l1 == 0) and (l2 == 0)) break;
cin >> l;
cin >> k;
vector < int> planks(k);
for (int i = 0 ; i < k ; i++)
cin >> planks[i];
sort(planks.begin(), planks.end());
aws1 = 0;
aws2 = 0;
if ((l2 * 100) % l == 0)
aws1 = answer(l1, l2 * 100 / l, planks);
if ((l1 * 100) % l == 0)
aws2 = answer(l2, l1 * 100 / l, planks);
if (aws1 == 0 && aws2 == 0)
cout << "impossivel" << endl;
else
{
if((aws1!=0)&&(aws2!=0))
cout << min(aws1, aws2) << endl;
else
cout << max(aws1,aws2) << endl;
}
}
return 0;
}
Input
100
10
1 2 2 2 2 3 3 4 4 5
5 4
100
7
4 5 4 4 4 4 3
4 5
99
4
4 4 4 4
3 2
100
7
2 4 1 4 2 4 4
0 0
Output
5
impossivel
impossivel
