Algorithm
Problem Name: beecrowd | 3166
Problem Link: https://www.beecrowd.com.br/judge/en/problems/view/3166
Finding Words on Main Diagonal
By Elder Sobrinho, UFTM  Brazil
Brazil
Timelimit: 3
In Algelandia, the favorite pastime is the Word Search puzzles. One of these has the following characteristics:
- The words occur only in the direction of the main diagonal;
- Words can occur with uppercase and/or lowercase;
- If a given word exists, it occurs only once and at any position on the diagonal;
- Words can exist in both normal and inverted form, that is, the diagonal reading could be top-down or bottom-up form.
In this context, the figure below demonstrates how the words “workshop”, “videogame” and “scanner” can occur in the game.
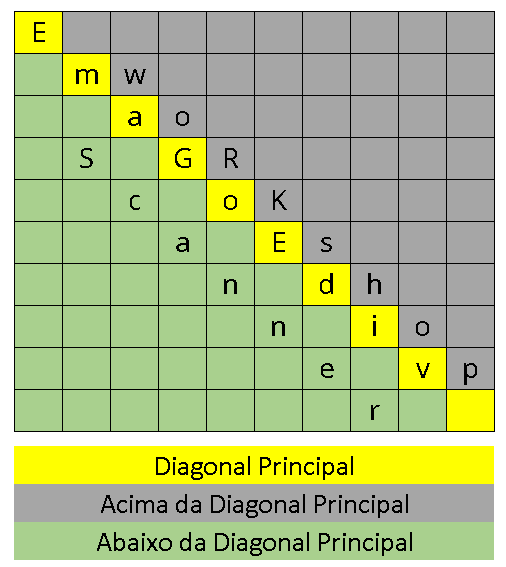
Input
The first line contains three integers: 1) N that represents the number of words that we will check if there are in the game, limited by [1,100]; 2) M that represents the number of lines in the matrix, limited by [10,1000]; 3) P that represents the number of columns in the matrix, limited by [10,1000]. In addition, each N-words follows the limit: [6,100].
Output
Depending on the existence of each N-word, inform:
- 1 Palavra "X" na diagonal principal
- 2 Palavra "X" acima da diagonal principal
- 3 Palavra "X" abaixo da diagonal principal
- 4 Palavra "X" inexistente
Where X is the searched word, moreover, X must be in lower case.
| Input Sample | Output Sample |
|
3 20 20 |
4 Palavra "google" inexistente |
Code Examples
#1 Code Example with Javascript Programming
Code -
Javascript Programming
const { readFileSync } = require("fs")
const input = readFileSync("/dev/stdin", "utf8").toLowerCase().split("\n")
const reverse = (str) => Array.from(str).reverse().join("")
class Matrix {
/**
* @param {number} rows
* @param {number} cols
*/
static createModel(rows = 0, cols = 0) { return ({ dimensions: { cols, rows } }) }
/**
* Create a square matrix from a object model
* @template T
* @param {ReturnType} model
* @param {Array} values
* @param {T} defaultReplacementValue
*/
static createFromModel(model, values, defaultReplacementValue = null) {
return Array.from({ length: model.dimensions.rows }, (_, rowIndex) => {
return Array.from({ length: model.dimensions.cols }, (_, colIndex) => {
return values[(model.dimensions.cols * rowIndex) + colIndex] || defaultReplacementValue
})
})
}
}
/** @param {string[][]} matrix */
function findsWordsRelativeToMainDiagonalFromMatrix(matrix) {
// A diagonal principal de uma matriz retangular é
// a diagonal que parte do canto superior esquerdo
// e segue a direita e abaixo até encontrar o lado
// direito ou o lado inferior da matriz.
const rows = matrix.length
const cols = matrix[0].length
const mainDiagonalCharSequence = Array.from({ length: Math.min(rows, cols) }, (_, i) => matrix[i][i]).join("")
const aboveMainDiagonalCharSequencesList = new Array(cols - 1).fill("")
const belowMainDiagonalCharSequencesList = new Array(rows - 1).fill("")
// ABOVE_MAIN_DIAGONAL_CHAR_SEQUENCES_LIST
for (let u = 1; u < = aboveMainDiagonalCharSequencesList.length; u++)
for (let i = 0, j = u; i < rows && j < cols; i++, j++)
aboveMainDiagonalCharSequencesList[u - 1] += matrix[i][j] || "0"
// BELOW MAIN DIAGONAL CHARACTER SEQUENCE LIST
for (let u = 1; u < = belowMainDiagonalCharSequencesList.length; u++)
for (let i = u, j = 0; i < rows && j < cols; i++, j++)
belowMainDiagonalCharSequencesList[u - 1] += matrix[i][j] || "0"
return (word = "") => {
word = word.toLowerCase()
const reversed = reverse(word)
if (mainDiagonalCharSequence.includes(word) || mainDiagonalCharSequence.includes(reversed)) return "MAIN DIAGONAL"
if (aboveMainDiagonalCharSequencesList.some(seq => seq.includes(word) || seq.includes(reversed))) return "ABOVE MAIN DIAGONAL"
if (belowMainDiagonalCharSequencesList.some(seq => seq.includes(word) || seq.includes(reversed))) return "BELOW MAIN DIAGONAL"
return "NOT FOUND"
}
}
function main() {
const output = []
const [numQueries, rows, cols] = input.shift().split(" ", 3).map(value => Number.parseInt(value, 10))
const words = input.splice(0, numQueries)
const chars = input.splice(0).map(row => row.split("", cols)).flat(1)
const squareMatrixModel = Matrix.createModel(rows, cols)
const matrix = Matrix.createFromModel(squareMatrixModel, chars, "")
const queriableMatrixSequencesInstance = findsWordsRelativeToMainDiagonalFromMatrix(matrix)
for (const word of words) {
const result = queriableMatrixSequencesInstance(word)
switch (result) {
case "MAIN DIAGONAL": { output.push(`1 Palavra "${word}" na diagonal principal`); break }
case "ABOVE MAIN DIAGONAL": { output.push(`2 Palavra "${word}" acima da diagonal principal`); break }
case "BELOW MAIN DIAGONAL": { output.push(`3 Palavra "${word}" abaixo da diagonal principal`); break }
case "NOT FOUND": { output.push(`4 Palavra "${word}" inexistente`); break }
}
}
console.log(output.join("\n"))
}
main()
/**
Conforme a existência de cada palavra N, informe:
1 Palavra "X" na diagonal principal
2 Palavra "X" acima da diagonal principal
3 Palavra "X" abaixo da diagonal principal
4 Palavra "X" inexistente
*/
Input
Output
