Algorithm
Problem Name: beecrowd | 2164
Problem Link: https://www.beecrowd.com.br/judge/en/problems/view/2164
Fast Fibonacci
By M.C. Pinto, UNILA 
Brazil
Timelimit: 1
Binet's formula is a way to calculate Fibonacci numbers.
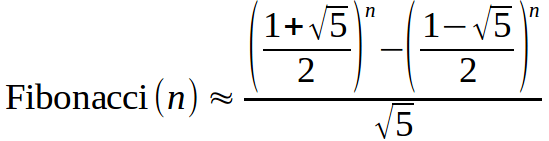
Your task is, given a natural number n, to compute the value of Fibonacci(n) using the formula above.
Input
The input is a natural number n (0 < n ≤ 50).
Output
The output is the value of Fibonacci(n) with 1 decimal place using the given Binet's formula.
| Input Samples | Output Samples |
|
1 |
1.0 |
|
2 |
1.0 |
|
3 |
2.0 |
Code Examples
#1 Code Example with C Programming
Code -
C Programming
#include <stdio.h>
#include <math.h>
int main(void)
{
int n;
double x, y, z;
scanf("%i", &n);
x=pow(((sqrt(5.0)+1)/2.0), n);
y=pow(((sqrt(5.0)-1)/2.0), n);
z=(x-y)/sqrt(5);
printf("%.1lf\n", x);
return 0;
}
Input
1
Output
1.0
#2 Code Example with C++ Programming
Code -
C++ Programming
#include <bits/stdc++.h>
using namespace std;
#define M 3.236067977
#define N -1.236067977
#define T 2.236067977
int main() {
int n,m;
double m1,n1;
cin >> n ;
m1 = ((pow((1+sqrt(5)),n) - pow(1-sqrt(5),n))/(pow(2,n)*sqrt(5)));
printf("%.1lf\n",m1);
return 0;
}
Input
1
Output
1.0
#3 Code Example with Javascript Programming
Code -
Javascript Programming
var input = require('fs').readFileSync('/dev/stdin', 'utf8');
var lines = input.split('\n');
var prompt = function(texto) { return lines.shift();};
const N = parseInt(prompt());
var term1 = Math.pow((1 + Math.sqrt(5)) / 2, N);
var term2 = Math.pow((1 - Math.sqrt(5)) / 2, N);
var fib = (term1 - term2) / Math.sqrt(5);
console.log(fib.toFixed(1));
Input
1
Output
1.0