Algorithm
Problem Name: 1028. Recover a Tree From Preorder Traversal
We run a preorder depth-first search (DFS) on the root of a binary tree.
At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node. If the depth of a node is D, the depth of its immediate child is D + 1. The depth of the root node is 0.
If a node has only one child, that child is guaranteed to be the left child.
Given the output traversal of this traversal, recover the tree and return its root.
Example 1:
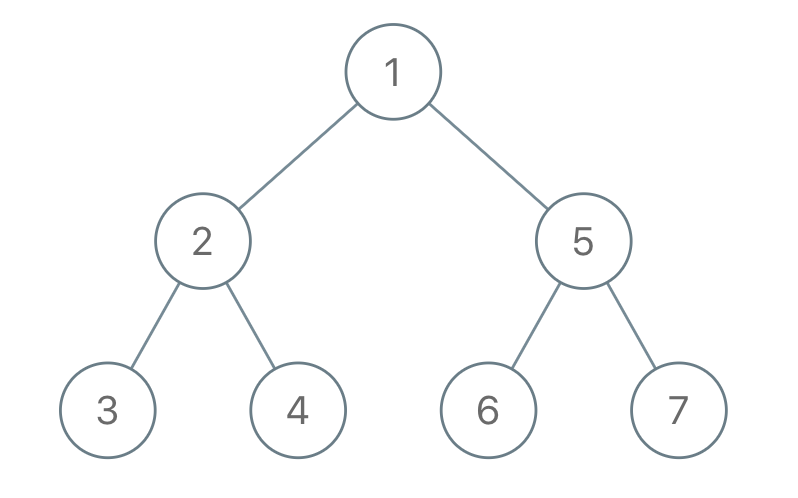
Input: traversal = "1-2--3--4-5--6--7" Output: [1,2,5,3,4,6,7]
Example 2:
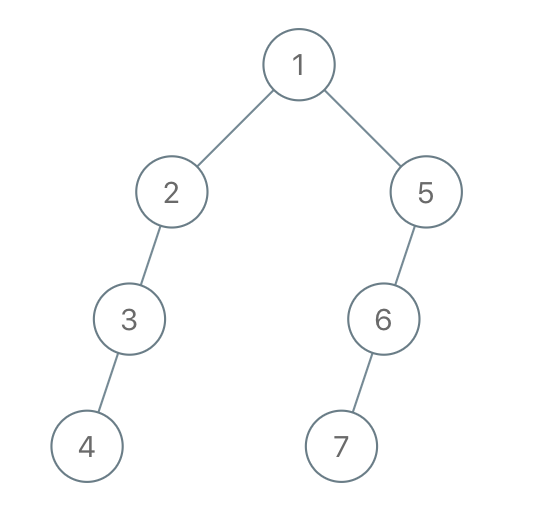
Input: traversal = "1-2--3---4-5--6---7" Output: [1,2,5,3,null,6,null,4,null,7]
Example 3:
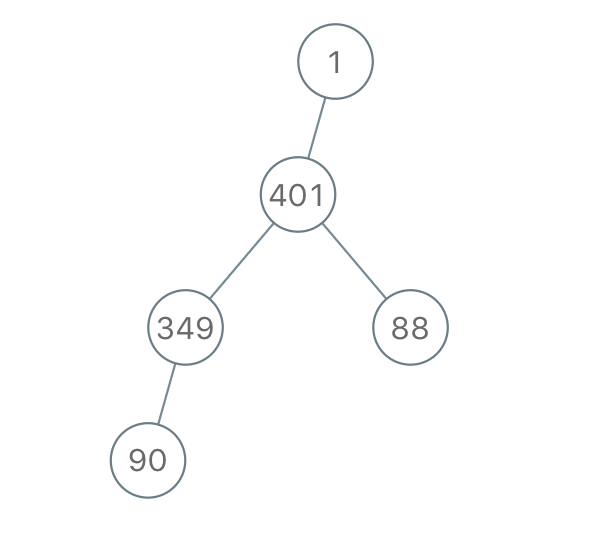
Input: traversal = "1-401--349---90--88" Output: [1,401,null,349,88,90]
Constraints:
- The number of nodes in the original tree is in the range
[1, 1000]. 1 <= Node.val <= 109
Code Examples
#1 Code Example with Java Programming
Code -
Java Programming
class Solution {
public TreeNode recoverFromPreorder(String S) {
Map map = new HashMap<>();
int idx = 0;
int n = S.length();
while (idx < n) {
int level = 0;
StringBuilder sb = new StringBuilder();
while (idx < n && S.charAt(idx) == '-') {
level++;
idx++;
}
while (idx < n && Character.isDigit(S.charAt(idx))) {
sb.append(S.charAt(idx++));
}
TreeNode currNode = new TreeNode(Integer.parseInt(sb.toString()));
map.put(level, currNode);
if (level > 0) {
TreeNode parent = map.get(level - 1);
if (parent.left == null) {
parent.left = currNode;
}
else {
parent.right = currNode;
}
}
}
return map.get(0);
}
}
Input
Output
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const recoverFromPreorder = function(S) {
const arr = []
let tmp = S[0]
for(let i = 1; i < S.length; i++) {
if(S[i] === '-') {
if(S[i-1] === '-') {
tmp += '-'
} else {
arr.push(tmp)
tmp = '-'
}
} else {
if(S[i-1] === '-') {
arr.push(tmp)
tmp = S[i]
} else {
tmp += S[i]
}
}
}
arr.push(tmp)
const resArr = []
helper(resArr, arr, 0)
return resArr[0]
};
function helper(nodeArr, strArr, idx) {
if(idx >= strArr.length) return
if(idx > 0) {
if(strArr[idx].startsWith('-')) {
helper(nodeArr, strArr, idx + 1)
} else {
nodeArr[idx] = new TreeNode(+strArr[idx])
let d = strArr[idx - 1].length
let tIdx
for(let i = idx - 1; ; i = i - 2) {
if(i>= 1) {
if(strArr[i].length < d) {
tIdx = i+1
break
}
} else {
tIdx = 0
break
}
}
if(nodeArr[tIdx].left) {
nodeArr[tIdx].right = nodeArr[idx]
} else {
nodeArr[tIdx].left = nodeArr[idx]
}
helper(nodeArr, strArr, idx + 1)
}
} else {
nodeArr[idx] = new TreeNode(+strArr[idx])
helper(nodeArr, strArr, idx + 1>
}
}
Input
Output
#3 Code Example with Python Programming
Code -
Python Programming
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def recoverFromPreorder(self, S: str) -> TreeNode:
def dfs(parent, s, lev):
print(parent.val, s, lev)
if not s: return
i = lev
l = 0
while i < len(s) and s[i].isdigit():
l = l * 10 + int(s[i])
i += 1
parent.left = TreeNode(l)
j = lev
f = '-' * lev
for ind in range(i, len(s)):
if s[ind:].startswith(f) and not s[ind:].startswith(f + '-') and s[ind -1] != '-':
rr = ind
j = ind + lev
r = 0
while j < len(s) and s[j].isdigit():
r = r * 10 + int(s[j])
j += 1
parent.right = TreeNode(r)
dfs(parent.left, s[i:rr], lev + 1)
dfs(parent.right, s[j:], lev + 1)
return
dfs(parent.left, s[i:], lev + 1)
i = num = 0
while i < len(S) and S[i].isdigit():
num = num * 10 + int(S[i])
i += 1
root = TreeNode(num)
dfs(root, S[i:], 1)
return root
Input
Output
