Algorithm
Problem Name: 1192. Critical Connections in a Network
There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [ai, bi] represents a connection between servers ai and bi. Any server can reach other servers directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some servers unable to reach some other server.
Return all critical connections in the network in any order.
Example 1:
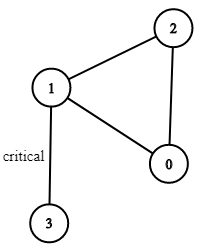
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]] Output: [[1,3]] Explanation: [[3,1]] is also accepted.
Example 2:
Input: n = 2, connections = [[0,1]] Output: [[0,1]]
Constraints:
2 <= n <= 105n - 1 <= connections.length <= 1050 <= ai, bi <= n - 1ai != bi- There are no repeated connections.
Code Examples
#1 Code Example with Java Programming
Code -
Java Programming
class Solution {
public List();
Map rank = new HashMap<>();
Set < String> connectionSet = new HashSet<>();
buildGraph(n, connections, graph, rank, connectionSet);
dfs(0, 0, graph, rank, connectionSet);
List < List();
for (String conn : connectionSet) {
int nodeOne = Integer.parseInt(conn.split("-")[0]);
int nodeTwo = Integer.parseInt(conn.split("-")[1]);
result.add(Arrays.asList(nodeOne, nodeTwo));
}
return result;
}
private void buildGraph(int n, List < List rank, Set connectionSet) {
for (int i = 0; i < n; i++) {
graph.put(i, new ArrayList < >());
rank.put(i, null);
}
for (List < Integer> edge : connections) {
graph.get(edge.get(0)).add(edge.get(1));
graph.get(edge.get(1)).add(edge.get(0));
connectionSet.add(
Math.min(edge.get(0), edge.get(1)) + "-" + Math.max(edge.get(0), edge.get(1)));
}
}
private int dfs(int node, int discoveryRank, Map < Integer, List rank, Set connectionSet) {
if (rank.get(node) != null) {
return rank.get(node);
}
rank.put(node, discoveryRank);
int minimumRank = discoveryRank + 1;
for (Integer neighbor : graph.get(node)) {
Integer neighborRank = rank.get(neighbor);
if (neighborRank != null && neighborRank == discoveryRank - 1) {
continue;
}
int recursiveRank = dfs(neighbor, discoveryRank + 1, graph, rank, connectionSet);
if (recursiveRank < = discoveryRank) {
connectionSet.remove(Math.min(node, neighbor) + "-" + Math.max(node, neighbor));
}
minimumRank = Math.min(minimumRank, recursiveRank);
}
return minimumRank;
}
}
Input
n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output
[[1,3]]
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const criticalConnections = function(n, connections) {
const g = [],
low = Array(n),
res = []
low.fill(0)
for (let con of connections) {
g[con[0]] = g[con[0]] || []
g[con[1]] = g[con[1]] || []
g[con[0]].push(con[1])
g[con[1]].push(con[0])
}
const dfs = function(cur, v, p) {
let dfn = cur
low[v] = cur
for (let i of g[v]) {
if (i != p) {
if (low[i] == 0) {
cur++
dfs(cur, i, v)
if (low[i] > dfn) {
res.push([i, v])
}
}
low[v] = Math.min(low[v], low[i])
}
}
}
dfs(1, 0, -1)
return res
}
Input
n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output
[[1,3]]
#3 Code Example with C# Programming
Code -
C# Programming
using System;
using System.Collections.Generic;
using System.Linq;
namespace LeetCode
{
public class _1192_CriticalConnectionsInANetwork
{
public IList < IList<int>> CriticalConnections(int n, IList < IList<int>> connections)
{
var graph = new Dictionary < int, IList<int>>();
var edges = new HashSet < (int, int)>();
foreach (var connection in connections)
{
if (!graph.ContainsKey(connection[0]))
graph[connection[0]] = new List<int>();
if (!graph.ContainsKey(connection[1]))
graph[connection[1]] = new List < int>();
graph[connection[0]].Add(connection[1]);
graph[connection[1]].Add(connection[0]);
edges.Add((connection[0], connection[1]));
}
var ranks = new int[n];
for (int i = 0; i < n; i++)
ranks[i] = -2;
DFS(0, 0, graph, edges, ranks, n);
return edges.Select(a => new int[2] { a.Item1, a.Item2 }).ToList < IList<int>>();
}
private int DFS(int node, int depth, Dictionary < int, IList<int>> graph, HashSet < (int, int)> edges, int[] ranks, int n)
{
if (ranks[node] >= 0) return ranks[node];
ranks[node] = depth;
var minStartPoint = n;
foreach (var neighbor in graph[node])
{
if (ranks[neighbor] == depth - 1) continue;
var startPoint = DFS(neighbor, depth + 1, graph, edges, ranks, n);
if (startPoint < = depth)
{
if (edges.Contains((node, neighbor)))
edges.Remove((node, neighbor));
else if (edges.Contains((neighbor, node)))
edges.Remove((neighbor, node));
}
minStartPoint = Math.Min(minStartPoint, startPoint);
}
return minStartPoint;
}
}
}
Input
n = 2, connections = [[0,1]]
Output
[[0,1]]