Algorithm
Problem Name: 218. The Skyline Problem
A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.
The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:
leftiis the x coordinate of the left edge of theithbuilding.rightiis the x coordinate of the right edge of theithbuilding.heightiis the height of theithbuilding.
You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
The skyline should be represented as a list of "key points" sorted by their x-coordinate in the form [[x1,y1],[x2,y2],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline's termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.
Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]
Example 1:
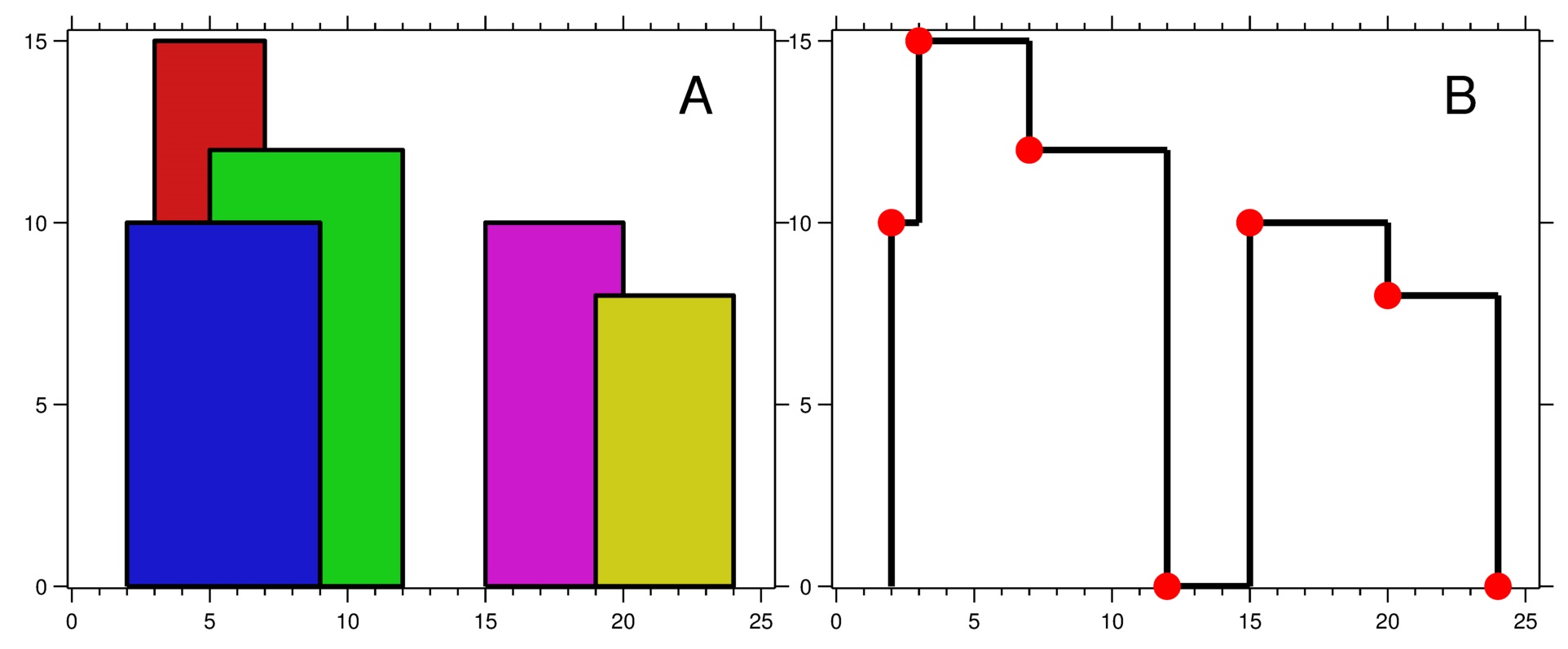
Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]] Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]] Explanation: Figure A shows the buildings of the input. Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.
Example 2:
Input: buildings = [[0,2,3],[2,5,3]] Output: [[0,3],[5,0]]
Constraints:
1 <= buildings.length <= 1040 <= lefti < righti <= 231 - 11 <= heighti <= 231 - 1buildingsis sorted byleftiin non-decreasing order.
Code Examples
#1 Code Example with C Programming
Code -
C Programming
typedef struct {
int x;
int h;
} dot_t;
typedef struct {
int *p;
int n;
int max;
} heap_t;
typedef struct {
int **p;
int sz;
int n;
} res_t;
int cmp(void const *a, void const *b) {
/* 1. ascending on x.
2. same on x, descending on height for left edge and
acesending on height for right edge.
* height of right edge are negative numbers, so
descending on height for both left and right edges.
*/
return ((dot_t *)a)->x < ((dot_t *)b)->x ? -1 :
((dot_t *)a)->x > ((dot_t *)b)->x ? 1 :
((dot_t *)b)->h < ((dot_t *)a)->h ? -1 : 1;
}
void res_init(res_t *res) {
res->sz = 100;
res->n = 0;
res->p = malloc(res->sz * sizeof(int *));
//assert(res->p);
}
void add2res(res_t *res, int x, int h) {
int *p = malloc(2 * sizeof(int));
//assert(p);
p[0] = x;
p[1] = h;
if (res->sz == res->n) {
res->sz *= 2;
res->p = realloc(res->p, res->sz * sizeof(int *));
//assert(res->p);
}
res->p[res->n ++] = p;
}
void heap_init(heap_t *heap, int sz) {
heap->n = 0;
heap->p = malloc(sz * sizeof(int));
heap->max = 0;
//assert(heap->p);
}
int add2heap(heap_t *heap, int k) {
heap->p[heap->n ++] = k;
if (k > heap->max) heap->max = k;
return heap->max;
}
int remove_heap(heap_t *heap, int k) {
// TODO: better to keep heap data are sorted.
int i, j, m = 0;
for (i = 0; i < heap->n; i ++) {
if (heap->p[i] == k) {
heap->p[i] = heap->p[-- heap->n];
if (heap->max == k) {
for (j = i; j < heap->n; j ++) {
if (m < heap->p[j]) m = heap->p[j];
}
heap->max = m;
}
return heap->max;
}
if (m < heap->p[i]) m = heap->p[i];
}
return heap->max;
}
int** getSkyline(int** buildings, int buildingsRowSize, int buildingsColSize, int* returnSize) {
dot_t *dots, *p;
res_t res;
heap_t heap;
int x1, x2, h, prev;
int n, i;
res_init(&res);
heap_init(&heap, buildingsRowSize + 1);
n = buildingsRowSize * 2;
dots = malloc(n * sizeof(dot_t));
//assert(dots);
// split all buildings to left and right dots
for (i = 0; i < buildingsRowSize; i ++) {
x1 = buildings[i][0];
x2 = buildings[i][1];
h = buildings[i][2];
p = &dots[i * 2 + 0];
p->x = x1;
p->h = h;
p = &dots[i * 2 + 1];
p->x = x2;
p->h = 0 - h;
}
qsort(dots, n, sizeof(dot_t), cmp);
prev = add2heap(&heap, 0);
// for each dot...
for (i = 0; i < n; i ++) {
p = &dots[i];
if (p->h > 0) {
// add p->h to heap
h = add2heap(&heap, p->h);
} else {
// remove p->h from heap
h = remove_heap(&heap, 0 - p->h);
}
if (prev != h) {
// there is a change on height
add2res(&res, p->x, h);
prev = h;
}
}
free(dots);
free(heap.p);
*returnSize = res.n;
return res.p;
}
Input
buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output
[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
#2 Code Example with Java Programming
Code -
Java Programming
class Solution {
public List();
List<int[]> heights = new ArrayList<>();
for (int[] building : buildings) {
heights.add(new int[]{building[0], -1 * building[2]});
heights.add(new int[]{building[1], 1 * building[2]});
}
Collections.sort(heights, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
PriorityQueue < Integer> pq = new PriorityQueue<>((a, b) -> b - a);
pq.add(0);
int previousMax = 0;
for (int[] height : heights) {
if (height[1] < 0) {
pq.add(-1 * height[1]);
} else {
pq.remove(height[1]);
}
int currentMax = pq.peek();
if (currentMax != previousMax) {
result.add(Arrays.asList(height[0], currentMax));
previousMax = currentMax;
}
}
return result;
}
}
Input
buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output
[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
#3 Code Example with Javascript Programming
Code -
Javascript Programming
const getSkyline = function getSkyline(
buildings,
begin = 0,
end = buildings.length
) {
if (begin === end) {
return []
} else if (end - begin === 1) {
const [Li, Ri, Hi] = buildings[begin]
return [[Li, Hi], [Ri, 0]]
} else {
const pivotIndex = begin + Math.ceil((end - begin) / 2)
return combineOutputs(
getSkyline(buildings, begin, pivotIndex),
getSkyline(buildings, pivotIndex, end)
)
}
}
function combineOutputs(a, b) {
let aIndex = 0
const aLength = a.length
let bIndex = 0
const bLength = b.length
let aHeight = 0
let bHeight = 0
const combined = []
while (aIndex < aLength || bIndex < bLength) {
if (aIndex < aLength && bIndex === bLength) {
return combined.concat(a.slice(aIndex))
} else if (bIndex < bLength && aIndex === aLength) {
return combined.concat(b.slice(bIndex))
} else {
const previousMax = Math.max(aHeight, bHeight)
const nextX = Math.min(a[aIndex][0], b[bIndex][0])
if (a[aIndex][0] === nextX) {
aHeight = a[aIndex][1]
aIndex++
}
if (b[bIndex][0] === nextX) {
bHeight = b[bIndex][1]
bIndex++
}
const newMax = Math.max(aHeight, bHeight)
if (newMax !== previousMax) {
combined.push([nextX, newMax])
}
}
}
return combined
}
Input
buildings = [[0,2,3],[2,5,3]]
Output
[[0,3],[5,0]]
#4 Code Example with Python Programming
Code -
Python Programming
class Solution:
def getSkyline(self, buildings):
events = sorted([(L, -H, R) for L, R, H in buildings] + list({(R, 0, None) for _, R, _ in buildings}))
res, hp = [[0, 0]], [(0, float("inf"))]
for x, negH, R in events:
while x >= hp[0][1]:
heapq.heappop(hp)
if negH:
heapq.heappush(hp, (negH, R))
if res[-1][1] + hp[0][0]:
res += [x, -hp[0][0]],
return res[1:]
Input
buildings = [[0,2,3],[2,5,3]]
Output
[[0,3],[5,0]]
#5 Code Example with C# Programming
Code -
C# Programming
using System;
using System.Collections.Generic;
namespace LeetCode
{
public class _0218_TheSkylineProblem
{
public IList < IList<int>> GetSkyline(int[][] buildings)
{
var sortedList = new SortedList < int, IList<int>>();
foreach (var building in buildings)
{
if (!sortedList.ContainsKey(building[0]))
sortedList.Add(building[0], new List < int>());
sortedList[building[0]].Add(-building[2]);
if (!sortedList.ContainsKey(building[1]))
sortedList.Add(building[1], new List < int>());
sortedList[building[1]].Add(building[2]);
}
var result = new List < IList<int>>();
var heights = new MaxPriorityQueue();
foreach (var x in sortedList.Keys)
{
foreach (var height in sortedList[x])
{
if (height < 0) heights.Insert(-height);
else heights.Delete(height);
}
if (heights.Size() == 0) result.Add(new List < int>() { x, 0 });
else
{
var height = heights.Max();
if (result.Count == 0 || result[result.Count - 1][1] != height)
result.Add(new List < int>() { x, height });
}
}
return result;
}
public class MaxPriorityQueue : PriorityQueue
{
public MaxPriorityQueue() : base() { }
public MaxPriorityQueue(int initCapacity) : base(initCapacity) { }
protected override void Sink(int k)
{
while (2 * k < = N)
{
int j = 2 * k;
if (j < N && pq[j] < pq[j + 1]) j++;
if (pq[k] >= pq[j]) break;
Swap(k, j);
k = j;
}
}
protected override void Swim(int k)
{
while (k > 1 && pq[k / 2] < pq[k])
{
Swap(k / 2, k);
k = k / 2;
}
}
public int Max() => First();
public int DeleteMax() => Delete();
}
public abstract class PriorityQueue
{
protected int N;
protected int[] pq;
public PriorityQueue() : this(1) { }
public PriorityQueue(int initCapacity)
{
this.N = 0;
pq = new int[initCapacity + 1];
}
public bool IsEmpty() => N == 0;
public int Size() => N;
public int First()
{
if (IsEmpty()) { throw new ArgumentOutOfRangeException(); }
return pq[1];
}
public void Insert(int x)
{
if (N >= pq.Length - 1)
Resize(pq.Length * 2);
pq[++N] = x;
Swim(N);
}
protected abstract void Swim(int k);
public int Delete()
{
var result = pq[1];
Swap(1, N--);
Sink(1);
pq[N + 1] = 0;
if (N > 0 && N == (pq.Length - 1) / 4)
Resize(pq.Length / 2);
return result;
}
public void Delete(int x)
{
var index = -1;
for (int i = 1; i < = N; i++)
{
if (pq[i] == x)
{
index = i;
break;
}
}
Swap(index, N--);
Sink(index);
pq[N + 1] = 0;
if (N > 0 && N == (pq.Length - 1) / 4)
Resize(pq.Length / 2);
}
protected abstract void Sink(int k);
private void Resize(int newCapacity)
{
var temp = new int[newCapacity + 1];
for (int i = 1; i < = N; i++)
temp[i] = pq[i];
pq = temp;
}
protected void Swap(int index1, int index2)
{
var temp = pq[index1];
pq[index1] = pq[index2];
pq[index2] = temp;
}
}
}
}
Input
buildings = [[0,2,3],[2,5,3]]
Output
[[0,3],[5,0]]