Algorithm
Problem Name: 913. Cat and Mouse
A game on an undirected graph is played by two players, Mouse and Cat, who alternate turns.
The graph is given as follows: graph[a] is a list of all nodes b such that ab is an edge of the graph.
The mouse starts at node 1 and goes first, the cat starts at node 2 and goes second, and there is a hole at node 0.
During each player's turn, they must travel along one edge of the graph that meets where they are. For example, if the Mouse is at node 1, it must travel to any node in graph[1].
Additionally, it is not allowed for the Cat to travel to the Hole (node 0.)
Then, the game can end in three ways:
- If ever the Cat occupies the same node as the Mouse, the Cat wins.
- If ever the Mouse reaches the Hole, the Mouse wins.
- If ever a position is repeated (i.e., the players are in the same position as a previous turn, and it is the same player's turn to move), the game is a draw.
Given a graph, and assuming both players play optimally, return
1if the mouse wins the game,2if the cat wins the game, or0if the game is a draw.
Example 1:
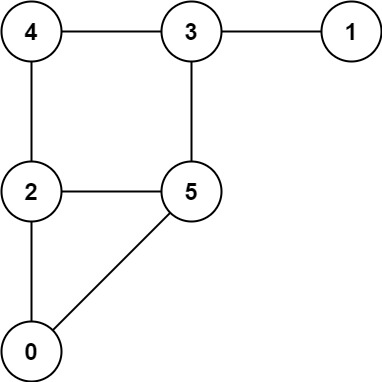
Input: graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] Output: 0
Example 2:
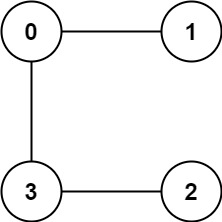
Input: graph = [[1,3],[0],[3],[0,2]] Output: 1
Constraints:
3 <= graph.length <= 501 <= graph[i].length < graph.length0 <= graph[i][j] < graph.lengthgraph[i][j] != igraph[i]is unique.- The mouse and the cat can always move.
Code Examples
#1 Code Example with Javascript Programming
Code -
Javascript Programming
const catMouseGame = function (g) {
const n = g.length
const win = Array(2)
.fill(0)
.map(() => Array(n * n).fill(0))
for (let i = 0; i < n; i++) {
win[0][i] = 1
win[1][i] = 1
}
for (let i = 1; i < n; i++) {
win[0][i * n + i] = 2
win[1][i * n + i] = 2
}
while (true) {
let anew = false
for (let m = 0; m < n; m++) {
inner: for (let c = 1; c < n; c++) {
if (win[0][m * n + c] == 0) {
let und = false
for (let e of g[m]) {
if (win[1][e * n + c] == 1) {
win[0][m * n + c] = 1
anew = true
continue inner
}
if (win[1][e * n + c] == 0) {
und = true
}
}
if (!und) {
win[0][m * n + c] = 2
anew = true
}
}
}
}
for (let c = 1; c < n; c++) {
inner: for (let m = 0; m < n; m++) {
if (win[1][m * n + c] == 0) {
let und = false
for (e of g[c]) {
if (e == 0) continue
if (win[0][m * n + e] == 2) {
win[1][m * n + c] = 2
anew = true
continue inner
}
if (win[0][m * n + e] == 0) {
und = true
}
}
if (!und) {
win[1][m * n + c] = 1
anew = true
}
}
}
}
if (!anew) break
}
return win[0][1 * n + 2]
}
Input
#2 Code Example with Python Programming
Code -
Python Programming
class Solution:
def catMouseGame(self, graph: 'List[List[int]]') -> 'int':
mouse_visited = [False] * len(graph)
mouse_win_map = [[None for column in range(len(graph))] for row in range(len(graph))]
cat_visited = [False] * len(graph)
cat_win_map = [[None for column in range(len(graph))] for row in range(len(graph))]
if self.isMouseWin(graph, 1, 2, mouse_visited, mouse_win_map):
return 1
elif self.isCatWin(graph, 1, 2, cat_visited, cat_win_map):
return 2
else:
return 0
def isMouseWin(self, graph, mouse, cat, mouse_visited, mouse_win_map):
if mouse == 0:
return True
if mouse_win_map[mouse][cat] is not None:
return mouse_win_map[mouse][cat]
mouse_visited[mouse] = True
for mouseMove in graph[mouse]:
if mouseMove == 0 or (mouseMove not in graph[cat] and mouseMove != cat):
if not mouse_visited[mouseMove]:
mouseWinFlag = True
for catMove in graph[cat]:
if catMove != 0 and not self.isMouseWin(graph, mouseMove, catMove, mouse_visited, mouse_win_map):
mouseWinFlag = False
break
if mouseWinFlag:
mouse_visited[mouse] = False
mouse_win_map[mouse][cat] = True
return True
mouse_visited[mouse] = False
mouse_win_map[mouse][cat] = False
return False
def isCatWin(self, graph, mouse, cat, cat_visited, cat_win_map):
if mouse == 0:
return False
if cat_win_map[mouse][cat] is not None:
return cat_win_map[mouse][cat]
cat_visited[cat] = True
for mouseMove in graph[mouse]:
if mouseMove == 0 or (mouseMove not in graph[cat] and mouseMove != cat):
catWinFlag = True
for catMove in graph[cat]:
if catMove != 0 and not cat_visited[catMove] and not self.isCatWin(graph, mouseMove, catMove,
cat_visited, cat_win_map):
catWinFlag = False
break
if not catWinFlag:
cat_visited[cat] = False
cat_win_map[mouse][cat] = False
return False
cat_visited[cat] = False
cat_win_map[mouse][cat] = True
return True
Input
#3 Code Example with C# Programming
Code -
C# Programming
using System.Collections.Generic;
using System.Linq;
namespace LeetCode
{
public class _0913_CatAndMouse
{
private const int DRAW = 0, MOUSE_WIN = 1, CAT_WIN = 2, MOUSE_TURN = 0, CAT_TURN = 1;
public int CatMouseGame(int[][] graph)
{
var N = graph.Length;
var degrees = new int[N, N, 2];
var colors = new int[N, N, 2];
var visited = new bool[N, N, 2];
for (int mouseIndex = 0; mouseIndex < N; mouseIndex++)
for (int catIndex = 0; catIndex < N; catIndex++)
{
degrees[mouseIndex, catIndex, MOUSE_TURN] = graph[mouseIndex].Length;
degrees[mouseIndex, catIndex, CAT_TURN] = graph[catIndex].Length;
if (graph[catIndex].Contains(0)) degrees[mouseIndex, catIndex, CAT_TURN]--;
}
var queue = new Queue < (int mouseIndex, int catIndex, int turn, int color)>();
for (int catIndex = 1; catIndex < N; catIndex++)
for (int turn = 0; turn < 2; turn++)
{
colors[0, catIndex, turn] = MOUSE_WIN;
queue.Enqueue((0, catIndex, turn, MOUSE_WIN));
visited[0, catIndex, turn] = true;
colors[catIndex, catIndex, turn] = CAT_WIN;
queue.Enqueue((catIndex, catIndex, turn, CAT_WIN));
visited[catIndex, catIndex, turn] = true;
}
while (queue.Count > 0)
{
(int mouseIndex, int catIndex, int turn, int color) = queue.Dequeue();
foreach (var parent in GetParents(graph, mouseIndex, catIndex, turn))
{
if (visited[parent.mouseIndex, parent.catIndex, parent.turn]) continue;
if (colors[parent.mouseIndex, parent.catIndex, parent.turn] == DRAW)
{
if ((parent.turn == MOUSE_TURN && color == MOUSE_WIN) || (parent.turn == CAT_TURN && color == CAT_WIN))
{
if (parent.mouseIndex == 1 && parent.catIndex == 2 && parent.turn == MOUSE_TURN)
return color;
colors[parent.mouseIndex, parent.catIndex, parent.turn] = color;
queue.Enqueue((parent.mouseIndex, parent.catIndex, parent.turn, color));
visited[parent.mouseIndex, parent.catIndex, parent.turn] = true;
}
else
{
degrees[parent.mouseIndex, parent.catIndex, parent.turn]--;
if (degrees[parent.mouseIndex, parent.catIndex, parent.turn] == 0)
{
var nextColor = parent.turn == MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
if (parent.mouseIndex == 1 && parent.catIndex == 2 && parent.turn == MOUSE_TURN)
return nextColor;
colors[parent.mouseIndex, parent.catIndex, parent.turn] = nextColor;
queue.Enqueue((parent.mouseIndex, parent.catIndex, parent.turn, nextColor));
visited[parent.mouseIndex, parent.catIndex, parent.turn] = true;
}
}
}
}
}
return colors[1, 2, MOUSE_TURN];
}
private IList < (int mouseIndex, int catIndex, int turn)> GetParents(int[][] graph, int mouseIndex, int catIndex, int turn)
{
var result = new List<(int mouseIndex, int catIndex, int turn)>();
if (turn == CAT_TURN)
foreach (var newMouseIndex in graph[mouseIndex])
result.Add((newMouseIndex, catIndex, MOUSE_TURN));
else
foreach (var newCatIndex in graph[catIndex])
if (newCatIndex > 0)
result.Add((mouseIndex, newCatIndex, CAT_TURN));
return result;
}
}
}
Input
Output
#4 Code Example with C Programming
Code -
C Programming
typedef struct {
int m; // mouse position
int c; // cat position
int t; // who is going to move in next turn
int s; // current win-lose state
} node_t;
#define MOUSE_POSITION(NODE) ((NODE)->m)
#define CAT_POSITION(NODE) ((NODE)->c)
#define MOUSE_MOVE 1
#define CAT_MOVE 2
#define IS_MOUSE_MOVE(NODE) ((NODE)->t == MOUSE_MOVE)
#define IS_CAT_MOVE(NODE) ((NODE)->t == CAT_MOVE)
#define UNKNOWN_ 0
#define MOUSE_WIN 1
#define CAT_WIN 2
#define SET_MOUSE_WIN(NODE) ((NODE)->s = MOUSE_WIN)
#define SET_CAT_WIN(NODE) ((NODE)->s = CAT_WIN)
#define IS_MOUSE_WIN(NODE) ((NODE)->s == MOUSE_WIN)
#define IS_CAT_WIN(NODE) ((NODE)->s == CAT_WIN)
#define MSZ 50
#define CSZ 50
#define TSZ 3
#define SIZE (MSZ * CSZ *TSZ)
#define IDX(M, C, T) ((M) * (CSZ) * (TSZ) + (C) * (TSZ) + T)
node_t *get_node(node_t *nodes, int m, int c, int t) {
node_t *node = &nodes[IDX(m, c, t)];
node->m = m;
node->c = c;
node->t = t;
return node;
}
bool mouse_win_on_all_children(node_t *node, node_t *nodes, int **graph, int *colsz) {
int i, j, k;
node_t *child;
i = CAT_POSITION(node);
for (j = 0; j < colsz[i]; j ++) {
k = graph[i][j];
if (k == 0) continue; // cat cannot go to position 0
child = get_node(nodes, MOUSE_POSITION(node), k, MOUSE_MOVE);
if (!IS_MOUSE_WIN(child)) return false; // not determined or cat wins
}
return true; // mouse wins on all children
}
bool cat_win_on_all_children(node_t *node, node_t *nodes, int **graph, int *colsz) {
int i, j, k;
node_t *child;
i = MOUSE_POSITION(node);
for (j = 0; j < colsz[i]; j ++) {
k = graph[i][j];
child = get_node(nodes, k, CAT_POSITION(node), CAT_MOVE);
if (!IS_CAT_WIN(child)) return false;
}
return true;
}
int catMouseGame(int** graph, int graphSize, int* graphColSize){
int i, j, k;
node_t nodes[SIZE] = { 0 }; // total number of nodes per (mouse position * cat position * who is going to move)
node_t *buff1[SIZE], *buff2[SIZE]; // queue of knowns states
node_t **q1 = buff1, **q2 = buff2, **q3;
int q1len = 0, q2len = 0;
node_t *node, *parent;
// initial known states
for (i = 1; i < graphSize; i ++) {
// mouse is at 0, regardless where cat is and who is going to move, mouse wins
node = get_node(nodes, 0, i, MOUSE_MOVE);
SET_MOUSE_WIN(node);
q1[q1len ++] = node; // enqeue this node
node = get_node(nodes, 0, i, CAT_MOVE);
SET_MOUSE_WIN(node);
q1[q1len ++] = node;
// mouse and cat have met, regardless who is going to move, cat wins
node = get_node(nodes, i, i, MOUSE_MOVE);
SET_CAT_WIN(node);
q1[q1len ++] = node;
node = get_node(nodes, i, i, CAT_MOVE);
SET_CAT_WIN(node);
q1[q1len ++] = node;
}
while (q1len) {
for (i = 0; i < q1len; i ++) {
node = q1[i];
// for each parent node which can move to current node
if (IS_MOUSE_MOVE(node)) { // current node is mouse going to move
j = CAT_POSITION(node); // parent must be cat was moving
for (k = 0; k < graphColSize[j]; k ++) {
if (graph[j][k] == 0) continue; // cat cannot be at position 0
parent = get_node(nodes, MOUSE_POSITION(node), graph[j][k], CAT_MOVE);
if (IS_MOUSE_WIN(parent) || IS_CAT_WIN(parent)) continue; // already determined
if (IS_CAT_WIN(node)) { // if cat wins at present, parent must win because:
SET_CAT_WIN(parent); // parent is cat to move so the cat can just move to here
} else if (mouse_win_on_all_children(parent, nodes, graph, graphColSize)) {
SET_MOUSE_WIN(parent);
} else {
parent = NULL; // unable to determine it, forget about it at this moment.
}
if (parent) q2[q2len ++] = parent; // enqueue it for next round expansion
}
} else { // current node is cat going to move
j = MOUSE_POSITION(node); // parent must be mouse was moving
for (k = 0; k < graphColSize[j]; k ++) {
parent = get_node(nodes, graph[j][k], CAT_POSITION(node), MOUSE_MOVE);
if (IS_MOUSE_WIN(parent) || IS_CAT_WIN(parent)) continue; // already determined
if (IS_MOUSE_WIN(node)) {
SET_MOUSE_WIN(parent);
} else if (cat_win_on_all_children(parent, nodes, graph, graphColSize)) {
SET_CAT_WIN(parent);
} else {
parent = NULL;
}
if (parent) q2[q2len ++] = parent; // enqueue it for next round expansion
}
}
}
// switch q1 and q2
q3 = q1;
q1 = q2;
q1len = q2len;
q2 = q3;
q2len = 0;
}
node = &nodes[IDX(1, 2, MOUSE_MOVE)];
return node->s;
}
Input
Output
