Algorithm
Problem Name: 363. Max Sum of Rectangle No Larger Than K
Given an m x n matrix matrix and an integer k, return the max sum of a rectangle in the matrix such that its sum is no larger than k.
It is guaranteed that there will be a rectangle with a sum no larger than k.
Example 1:
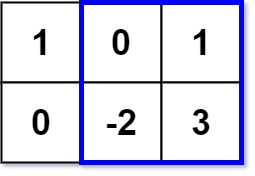
Input: matrix = [[1,0,1],[0,-2,3]], k = 2 Output: 2 Explanation: Because the sum of the blue rectangle [[0, 1], [-2, 3]] is 2, and 2 is the max number no larger than k (k = 2).
Example 2:
Input: matrix = [[2,2,-1]], k = 3 Output: 3
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-100 <= matrix[i][j] <= 100-105 <= k <= 105
Code Examples
#1 Code Example with C Programming
Code -
C Programming
int lower_bound(int *set, int len, int x) {
int i;
for (i = 0; i < len; i ++) {
if (set[i] >= x) break; // first one not less than k
}
return i;
}
int maxSumSubmatrix(int** matrix, int matrixRowSize, int matrixColSize, int k) {
int *sum_on_row, sum, max;
int *predecessor, len, i, j;
int left, right, row;
int *buff;
buff = malloc((matrixRowSize * 2 + 1) * sizeof(int));
//assert(buff);
sum_on_row = &buff[0];
predecessor = &buff[matrixRowSize];
max = 0x80000000;
for (left = 0; left < matrixColSize; left ++) {
memset(sum_on_row, 0, matrixRowSize * sizeof(int));
for (right = left; right < matrixColSize; right ++) {
len = 0;
predecessor[len ++] = 0;
sum = 0;
for (row = 0; row < matrixRowSize; row ++) {
sum_on_row[row] += matrix[row][right];
sum += sum_on_row[row];
// find max sum no larger than k
i = lower_bound(predecessor, len, sum - k);
if (i < len) {
if (max < sum - predecessor[i]) {
max = sum - predecessor[i];
}
}
i = lower_bound(predecessor, len, sum);
for (j = len; j > i; j --) {
predecessor[j] = predecessor[j - 1];
}
/*if (i < len) {
memcpy(&predecessor[i + 1], &predecessor[i], (len - i) * sizeof(int));
}*/
predecessor[i] = sum;
len ++;
}
}
}
free(buff);
return max;
}
Input
matrix = [[1,0,1],[0,-2,3]], k = 2
Output
2
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const maxSumSubmatrix = function(matrix, k) {
const row = matrix.length,
col = matrix[0].length
let result = -Infinity
for (let i = 0; i < col; i++) {
let rowSum = Array(row).fill(0)
for (let j = i; j < col; j++) {
let sum = 0,
max = -Infinity
for (let r = 0; r < row; r++) {
rowSum[r] += matrix[r][j]
if (sum < 0) sum = 0
sum += rowSum[r]
max = Math.max(max, sum)
}
if (max <= k) result = Math.max(result, max)
else {
max = -Infinity
for (let m = 0; m < row; m++) {
sum = 0
for (let n = m; n < row; n++) {
sum += rowSum[n]
if (sum <= k) max = Math.max(max, sum)
}
}
result = Math.max(result, max)
}
if (result === k) return k
}
}
return result
}
Input
matrix = [[1,0,1],[0,-2,3]], k = 2
Output
2
#3 Code Example with Python Programming
Code -
Python Programming
class Solution:
def maxSumSubmatrix(self, matrix, k, mxTotal = -float("inf")):
for l in range(len(matrix[0])):
dp = [0] * len(matrix)
for r in range(l, len(matrix[0])):
for i in range(len(matrix)):
dp[i] += matrix[i][r]
sums, cur, mx = [float("inf")], 0, -float("inf")
for sm in dp:
bisect.insort(sums, cur)
cur += sm
mx = max(mx, cur - sums[bisect.bisect_left(sums, cur - k)])
mxTotal = max(mxTotal, mx)
return mxTotal
Input
matrix = [[2,2,-1]], k = 3
Output
3