Algorithm
Problem Name: 894. All Possible Full Binary Trees
Given an integer n, return a list of all possible full binary trees with n nodes. Each node of each tree in the answer must have Node.val == 0.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order.
A full binary tree is a binary tree where each node has exactly 0 or 2 children.
Example 1:
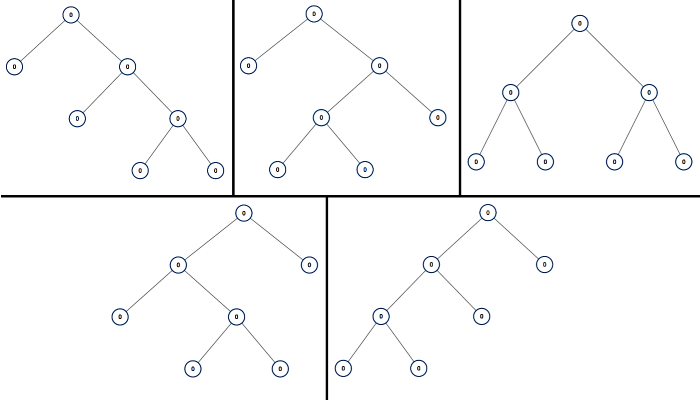
Input: n = 7 Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
Example 2:
Input: n = 3 Output: [[0,0,0]]
Constraints:
1 <= n <= 20
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
class Solution {
public:
vector<TreeNode*> allPossibleFBT(int N) {
vector<TreeNode*> res;
if (N == 1) {
res.push_back(new TreeNode(0));
return res;
}
--N;
for (int i = 1; i < N; i += 2) {
auto left = allPossibleFBT(i);
auto right = allPossibleFBT(N - i);
for (TreeNode* l: left) {
for (TreeNode* r: right) {
TreeNode* cur = new TreeNode(0);
cur->left = l;
cur->right = r;
res.push_back(cur);
}
}
}
return res;
}
};
Input
Output
#2 Code Example with Java Programming
Code -
Java Programming
class Solution {
public List allPossibleFBT(int n) {
Map();
return allPossibleFBTHelper(n, dp);
}
private List < TreeNode> allPossibleFBTHelper(int n, Map result = new ArrayList<>();
if (n == 1) {
result.add(new TreeNode(0));
} else if (n % 2 == 1) {
for (int i = 0; i < n; i++) {
int j = n - 1 - i;
for (TreeNode left : allPossibleFBTHelper(i, dp)) {
for (TreeNode right : allPossibleFBTHelper(j, dp)) {
TreeNode root = new TreeNode(0);
root.left = left;
root.right = right;
result.add(root);
}
}
}
}
dp.put(n, result);
return dp.get(n);
}
}
Input
Output
#3 Code Example with Javascript Programming
Code -
Javascript Programming
const allPossibleFBT = function(N) {
if (N <= 0) return []
const dp = Array.from({ length: N + 1 }, () => [])
dp[1].push(new TreeNode(0))
for (let numNode = 1; numNode < = N; numNode += 2) {
for (let leftNode = 1; leftNode < numNode; leftNode += 2) {
for (let left of dp[leftNode]) {
for (let right of dp[numNode - 1 - leftNode]) {
let root = new TreeNode(0)
root.left = left
root.right = right
dp[numNode].push(root)
}
}
}
}
return dp[N]
};
Input
Output
#4 Code Example with Python Programming
Code -
Python Programming
class Solution:
def allPossibleFBT(self, N):
def constr(N):
if N == 1: yield TreeNode(0)
for i in range(1, N, 2):
for l in constr(i):
for r in constr(N - i - 1):
m = TreeNode(0)
m.left = l
m.right = r
yield m
return list(constr(N))
Input
Output
#5 Code Example with C# Programming
Code -
C# Programming
using System.Collections.Generic;
namespace LeetCode
{
public class _0894_AllPossibleFullBinaryTrees
{
public IList < TreeNode> AllPossibleFBT(int N)
{
var cache = new Dictionary<int, IList AllPossibleFBT(int n, Dictionary<int, IList();
if (cache.ContainsKey(n)) return cache[n];
if (n == 1)
{
cache[n] = new List < TreeNode>() { new TreeNode(0) };
return cache[n];
}
var results = new List < TreeNode>();
for (int left = 1; left < n; left += 2)
{
int right = n - 1 - left;
foreach (var leftNode in AllPossibleFBT(left))
foreach (var rightNode in AllPossibleFBT(right))
{
var root = new TreeNode(0);
root.left = leftNode;
root.right = rightNode;
results.Add(root);
}
}
cache[n] = results;
return cache[n];
}
}
}
Input
Output
