Algorithm
Problem Name: 587. Erect the Fence
Problem Link: https://leetcode.com/problems/erect-the-fence/
You are given an array trees where trees[i] = [xi, yi] represents the location of a tree in the garden.
Fence the entire garden using the minimum length of rope, as it is expensive. The garden is well-fenced only if all the trees are enclosed.
Return the coordinates of trees that are exactly located on the fence perimeter. You may return the answer in any order.
Example 1:
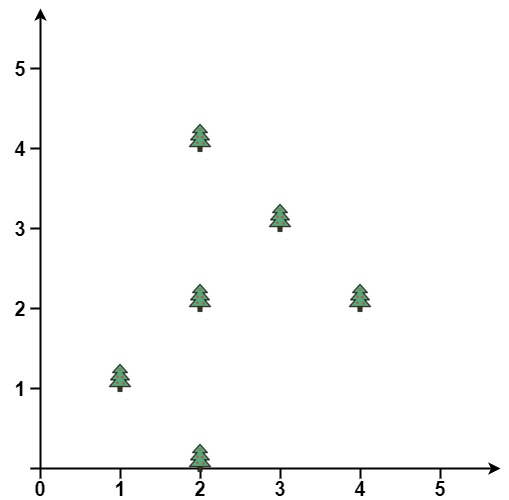
Input: trees = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]] Output: [[1,1],[2,0],[4,2],[3,3],[2,4]] Explanation: All the trees will be on the perimeter of the fence except the tree at [2, 2], which will be inside the fence.
Example 2:
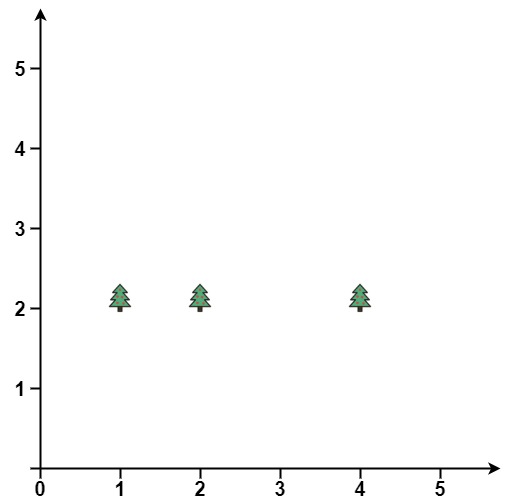
Input: trees = [[1,2],[2,2],[4,2]] Output: [[4,2],[2,2],[1,2]] Explanation: The fence forms a line that passes through all the trees.
Constraints:
1 <= trees.length <= 3000trees[i].length == 20 <= xi, yi <= 100- All the given positions are unique.
Code Examples
#1 Code Example with C Programming
Code -
C Programming
const outerTrees = function (points) {
const orientation = (p1, p2, p3) => {
return (p2[1] - p1[1]) * (p3[0] - p2[0]) - (p2[0] - p1[0]) * (p3[1] - p2[1])
}
points.sort((a, b) => {
return a[0] === b[0] ? a[1] - b[1] : a[0] - b[0]
})
const stack = []
for (let i = 0; i < points.length; i++) {
while (
stack.length >= 2 &&
orientation(stack[stack.length - 2], stack[stack.length - 1], points[i]) >
0
)
stack.pop()
stack.push(points[i])
}
stack.pop()
for (let i = points.length - 1; i >= 0; i--) {
while (
stack.length >= 2 &&
orientation(stack[stack.length - 2], stack[stack.length - 1], points[i]) >
0
)
stack.pop()
stack.push(points[i])
}
return [...new Set(stack)]
}
Input
trees = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output
[[1,1],[2,0],[4,2],[3,3],[2,4]]
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const outerTrees = function (points) {
const orientation = (p1, p2, p3) => {
return (p2[1] - p1[1]) * (p3[0] - p2[0]) - (p2[0] - p1[0]) * (p3[1] - p2[1])
}
points.sort((a, b) => {
return a[0] === b[0] ? a[1] - b[1] : a[0] - b[0]
})
const stack = []
for (let i = 0; i < points.length; i++) {
while (
stack.length >= 2 &&
orientation(stack[stack.length - 2], stack[stack.length - 1], points[i]) >
0
)
stack.pop()
stack.push(points[i])
}
stack.pop()
for (let i = points.length - 1; i >= 0; i--) {
while (
stack.length >= 2 &&
orientation(stack[stack.length - 2], stack[stack.length - 1], points[i]) >
0
)
stack.pop()
stack.push(points[i])
}
return [...new Set(stack)]
}
Input
trees = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output
[[1,1],[2,0],[4,2],[3,3],[2,4]]
#3 Code Example with Python Programming
Code -
Python Programming
class Solution(object):
def outerTrees(self, points):
"""Computes the convex hull of a set of 2D points.
Input: an iterable sequence of (x, y) pairs representing the points.
Output: a list of vertices of the convex hull in counter-clockwise order,
starting from the vertex with the lexicographically smallest coordinates.
Implements Andrew's monotone chain algorithm. O(n log n) complexity.
"""
# Sort the points lexicographically (tuples are compared lexicographically).
# Remove duplicates to detect the case we have just one unique point.
# points = sorted(set(points))
points = sorted(points, key=lambda p: (p.x, p.y))
# Boring case: no points or a single point, possibly repeated multiple times.
if len(points) <= 1:
return points
# 2D cross product of OA and OB vectors, i.e. z-component of their 3D cross product.
# Returns a positive value, if OAB makes a counter-clockwise turn,
# negative for clockwise turn, and zero if the points are collinear.
def cross(o, a, b):
# return (a[0] - o[0]) * (b[1] - o[1]) - (a[1] - o[1]) * (b[0] - o[0])
return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x)
# Build lower hull
lower = []
for p in points:
while len(lower) >= 2 and cross(lower[-2], lower[-1], p) < 0:
lower.pop()
lower.append(p)
# Build upper hull
upper = []
for p in reversed(points):
while len(upper) >= 2 and cross(upper[-2], upper[-1], p) < 0:
upper.pop()
upper.append(p)
# Concatenation of the lower and upper hulls gives the convex hull.
# Last point of each list is omitted because it is repeated at the
# beginning of the other list.
# return lower[:-1] + upper[:-1]
return list(set(lower[:-1] + upper[:-1]))
Input
trees = [[1,2],[2,2],[4,2]]
Output
[[4,2],[2,2],[1,2]]