Algorithm
Problem Name: 787. Cheapest Flights Within K Stops
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1:
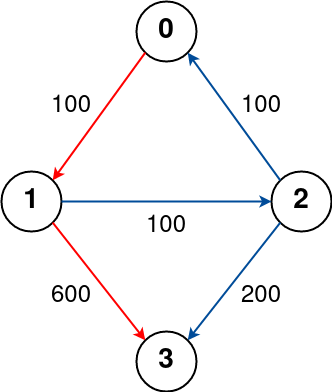
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1 Output: 700 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.
Example 2:
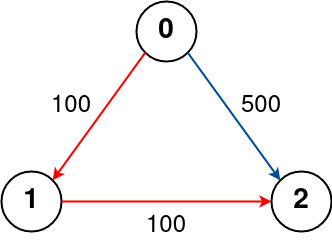
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
Example 3:
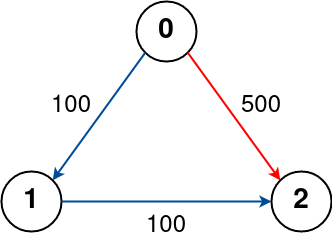
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown above. The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
Constraints:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- There will not be any multiple flights between two cities.
0 <= src, dst, k < nsrc != dst
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
// DFS + Brute Force
class Solution {
public:
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
int minPrice = INT_MAX;
vector < vector<vector<int>>>g(n);
for(auto v: flights) g[v[0]].push_back({v[1], v[2]});
dfs(g, src, dst, K, 0, minPrice);
return minPrice == INT_MAX ? -1 : minPrice;
}
void dfs(vector < vector<vector<int>>>& g, int cur, int dst, int K, int price, int& minPrice){
if(cur == dst){
minPrice = min(minPrice, price);
return;
}
if(K == -1 || price >= minPrice) return;
for(auto v: g[cur]) dfs(g, v[0], dst, K - 1, price + v[1], minPrice);
}
};
// BFS + Priority_queue
class Solution {
public:
int findCheapestPrice(int n, vector<vector < int>>& flights, int src, int dst, int K) {
vector < vector<int>>g(101);
vector < vector<int>>w(101, vector<int>(101));
for (auto& v: flights) {
int a = v[0]; // src
int b = v[1]; // dst
int c = v[2]; // weight
g[a].push_back(b);
w[a][b] = c;
}
auto comp = [](vector<int>& v1, vector<int>& v2> {
return v1[1] > v2[1];
};
priority_queue < vector<int>, vector < vector<int>>, decltype(comp)>pq(comp);
pq.push({src, 0, K});
while (!pq.empty()) {
auto v = pq.top();
pq.pop();
int from = v[0];
int cost = v[1];
int stop = v[2];
if (from == dst) {
return cost;
}
if (stop < 0) {
continue;
}
--stop;
for (int x: g[from]) {
pq.push({x, cost + w[from][x], stop});
}
}
return -1;
}
};
Input
Output
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const findCheapestPrice = function(n, flights, src, dst, K) {
let mn = new Array(n + 1).fill(Infinity);
mn[src] = 0;
for(let k = 0; k < K + 1; k++){
let newmn = [].concat(mn);
for(let i = 0; i < flights.length; i++){
let f = flights[i], a = f[0], b = f[1], c = f[2];
newmn[b] = Math.min(newmn[b], mn[a] + c);
}
mn = [].concat(newmn);
}
return mn[dst] != Infinity ? mn[dst] : -1
}
Input
Output
#3 Code Example with Python Programming
Code -
Python Programming
class Solution:
def findCheapestPrice(self, n, flights, src, dst, K):
flight = collections.defaultdict(list)
for s, e, p in flights:
flight[s].append((e, p))
heap = [(0, src, K + 1)]
while heap:
price, city, stop = heapq.heappop(heap)
if city == dst:
return price
elif stop > 0:
for c, p in flight[city]:
heapq.heappush(heap, (price + p, c, stop - 1))
return -1
Input
Output
#4 Code Example with C# Programming
Code -
C# Programming
using System;
namespace LeetCode
{
public class _0787_CheapestFlightsWithinKStops
{
public int FindCheapestPrice(int n, int[][] flights, int src, int dst, int K)
{
var costs = new int[n];
for (int i = 0; i < n; i++)
costs[i] = int.MaxValue / 2;
costs[src] = 0;
for (int i = 0; i < = K; i++)
{
var currentCost = new int[n];
Array.Copy(costs, currentCost, n);
foreach (var flight in flights)
{
if (currentCost[flight[1]] > costs[flight[0]] + flight[2])
currentCost[flight[1]] = costs[flight[0]] + flight[2];
}
costs = currentCost;
}
return costs[dst] == int.MaxValue / 2 ? -1 : costs[dst];
}
}
}
Input
Output
