Algorithm
Problem Name: 919. Complete Binary Tree Inserter
Problem Link: https://leetcode.com/problems/complete-binary-tree-inserter/
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the CBTInserter class:
CBTInserter(TreeNode root)Initializes the data structure with therootof the complete binary tree.int insert(int v)Inserts aTreeNodeinto the tree with valueNode.val == valso that the tree remains complete, and returns the value of the parent of the insertedTreeNode.TreeNode get_root()Returns the root node of the tree.
Example 1:
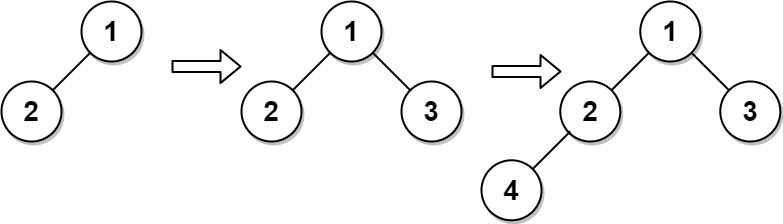
Input ["CBTInserter", "insert", "insert", "get_root"] [[[1, 2]], [3], [4], []] Output [null, 1, 2, [1, 2, 3, 4]] Explanation CBTInserter cBTInserter = new CBTInserter([1, 2]); cBTInserter.insert(3); // return 1 cBTInserter.insert(4); // return 2 cBTInserter.get_root(); // return [1, 2, 3, 4]
Constraints:
- The number of nodes in the tree will be in the range
[1, 1000]. 0 <= Node.val <= 5000rootis a complete binary tree.0 <= val <= 5000- At most
104calls will be made toinsertandget_root.
Code Examples
#1 Code Example with Java Programming
Code -
Java Programming
class CBTInserter {
TreeNode root;
Deque < TreeNode> deque;
public CBTInserter(TreeNode root) {
this.root = root;
deque = new LinkedList < >();
Queue queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode node = queue.remove();
if (node.left == null || node.right == null) {
deque.addLast(node);
}
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
public int insert(int v) {
TreeNode node = deque.peekFirst();
deque.addLast(new TreeNode(v));
if (node.left == null) {
node.left = deque.peekLast();
}
else {
node.right = deque.peekLast();
deque.removeFirst();
}
return node.val;
}
public TreeNode get_root() {
return root;
}
}
Input
["CBTInserter", "insert", "insert", "get_root"]
[[[1, 2]], [3], [4], []]
Output
[null, 1, 2, [1, 2, 3, 4]]
#2 Code Example with Javascript Programming
Code -
Javascript Programming
var CBTInserter = function(root) {
this.r = root
};
CBTInserter.prototype.insert = function(val) {
let q = [this.r]
while(q.length) {
const tmp = []
for(let i = 0; i < q.length; i++) {
const cur = q[i]
if(cur.left == null) {
cur.left = new TreeNode(val)
return cur.val
} else tmp.push(cur.left)
if(cur.right == null) {
cur.right = new TreeNode(val)
return cur.val
} else tmp.push(cur.right)
}
q = tmp
}
};
CBTInserter.prototype.get_root = function() {
return this.r
};
Input
["CBTInserter", "insert", "insert", "get_root"]
[[[1, 2]], [3], [4], []]
Output
[null, 1, 2, [1, 2, 3, 4]]
#3 Code Example with Python Programming
Code -
Python Programming
class CBTInserter:
def __init__(self, root):
self.arr, q = [], [root]
while q:
self.arr += [node for node in q]
q = [child for node in q for child in (node.left, node.right) if child]
def insert(self, v):
parent = self.arr[(len(self.arr) - 1) // 2]
if not len(self.arr) % 2:
child = parent.right = TreeNode(v)
else:
child = parent.left = TreeNode(v)
self.arr += [child]
return parent.val
def get_root(self):
return self.arr[0]
Input
["CBTInserter", "insert", "insert", "get_root"]
[[[1, 2]], [3], [4], []]
Output
[null, 1, 2, [1, 2, 3, 4]]