Algorithm
Problem Name: 74. Search a 2D Matrix
You are given an m x n integer matrix matrix with the following two properties:
- Each row is sorted in non-decreasing order.
- The first integer of each row is greater than the last integer of the previous row.
Given an integer target, return true if target is in matrix or false otherwise.
You must write a solution in O(log(m * n)) time complexity.
Example 1:
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 Output: true
Example 2:
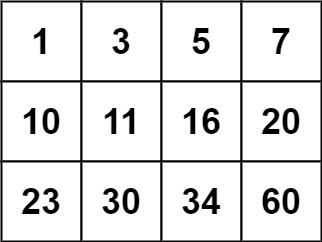
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
Code Examples
#1 Code Example with C Programming
Code -
C Programming
bool searchMatrix(int** matrix, int matrixRowSize, int matrixColSize, int target) {
int s, x, z, y, mr, mc;
int a, b, c;
s = 0; x = matrixRowSize - 1;
while (s < = x) {
mr = s + (x - s) / 2;
a = matrix[mr][0];
b = matrix[mr][matrixColSize - 1];
if (target >= a && target < = b) {
z = 0; y = matrixColSize - 1;
while (z < = y) {
mc = z + (y - z) / 2;
c = matrix[mr][mc];
if (target == c) return true;
if (target < c) y = mc - 1;
else z = mc + 1;
}
return false;
}
if (target < a) x = mr - 1;
else s = mr + 1;
}
return false;
}
Input
matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output
true
#2 Code Example with C++ Programming
Code -
C++ Programming
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if(matrix.empty()) return false;
int lo = 0, hi = matrix.size() - 1;
int mid = lo + (hi - lo) / 2 + 1;
while(lo < hi>{
if(matrix[mid][0] > target) hi = mid - 1;
else lo = mid;
mid = lo + (hi - lo) / 2 + 1;
}
auto p = lower_bound(matrix[lo].begin(), matrix[lo].end(), target);
return p != matrix[lo].end() && *p == target;
}
};
Input
matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output
true
#3 Code Example with Java Programming
Code -
Java Programming
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int rowIdx = matrix.length - 1;
int colIdx = matrix[0].length - 1;
while (rowIdx >= 0 && colIdx >= 0) {
if (matrix[rowIdx][colIdx] == target) {
return true;
}
if (matrix[rowIdx][colIdx] > target) {
colIdx--;
if (colIdx < 0) {
colIdx = matrix[0].length - 1;
rowIdx--;
}
} else {
rowIdx--;
}
}
return false;
}
}
Input
matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output
true
#4 Code Example with Javascript Programming
Code -
Javascript Programming
const searchMatrix = function(matrix, target) {
const rows = matrix.length
const cols = (matrix[0] || []).length
const r = chkRow(matrix, rows, cols, target)
if(r === -1) return false
for(let i = 0; i < cols; i++) {
if(matrix[r][i] === target) return true
}
return false
};
function chkRow(matrix, rows, cols, target) {
if(cols < = 0) return -1
for(let i = 0; i < rows; i++) {
if(target <= matrix[i][cols - 1]> return i
}
return -1
}
Input
matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output
false
#5 Code Example with Python Programming
Code -
Python Programming
class Solution:
def searchMatrix(self, matrix, target):
ls = list(itertools.chain(*matrix))
return ls and ls[bisect.bisect(ls, target) - 1] == target or False
Input
matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output
false
#6 Code Example with C# Programming
Code -
C# Programming
namespace LeetCode
{
public class _074_SearchA2DMatrix
{
public bool SearchMatrix(int[][] matrix, int target)
{
if (matrix.Length == 0) return false;
int columnLength = matrix[0].Length;
int lo = 0, hi = matrix.Length * columnLength - 1;
int i, j;
while (lo < = hi)
{
var mid = lo + (hi - lo) / 2;
i = mid / columnLength;
j = mid % columnLength;
if (matrix[i][j] < target) { lo = mid + 1; }
else if (matrix[i][j] > target) { hi = mid - 1; }
else { return true; }
}
return false;
}
}
}
Input
matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output
true