Algorithm
Problem Name: 240. Search a 2D Matrix II
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 Output: true
Example 2:
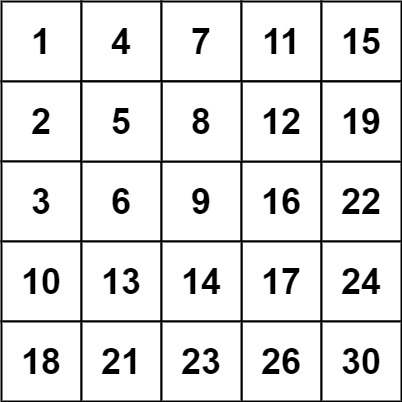
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
-109 <= target <= 10
Code Examples
#1 Code Example with C Programming
Code -
C Programming
bool search(int** matrix, int top, int left, int bottom, int right, int target) {
int row, col;
int i;
if (target < matrix[top][left] ||
target > matrix[bottom][right]) return false;
if (top == bottom) {
// can use binary search
for (i = left; i < = right; i ++) {
if (matrix[top][i] == target) return true;
}
return false;
}
if (left == right) {
// can use binary search
for (i = top; i < = bottom; i ++) {
if (matrix[i][left] == target) return true;
}
return false;
}
row = top + (bottom - top) / 2;
col = left + (right - left) / 2;
if (target == matrix[row][col]) return true;
if (target < matrix[row][col]) return (search(matrix, top, left, row, right, target) ||
search(matrix, row + 1, left, bottom, col - 1, target));
return (search(matrix, row + 1, left, bottom, right, target) ||
search(matrix, top, col + 1, row, right, target));
}
bool searchMatrix(int** matrix, int matrixRowSize, int matrixColSize, int target) {
#if 0 // 100+ ms
return search(matrix, 0, 0, matrixRowSize - 1, matrixColSize - 1, target);
#else // 40+ ms
int r = 0;
int c = matrixColSize - 1;
while (r < = matrixRowSize - 1 &&
c >= 0) {
if (matrix[r][c] == target) return true;
if (matrix[r][c] < target) r ++;
else c --;
}
return false;
#endif
}
Input
matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output
true
#2 Code Example with C++ Programming
Code -
C++ Programming
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if(matrix.empty() || matrix[0].empty()) return false;
int lo = BS(matrix, 0, target), hi = BS(matrix, matrix[0].size() - 1, target);
for(int i = min(lo, hi); i <= max(lo, hi); i++){
auto it = lower_bound(matrix[i].begin(), matrix[i].end(), target);
if(it != matrix[i].end() && *it == target) return true;
}
return false;
}
int BS(vector < vector<int>>& matrix, int col, int target){
int lo = 0, hi = matrix.size() - 1, mid = lo + (hi - lo) / 2;
while(lo < = hi>{
if(matrix[mid][col] > target) hi = mid - 1;
else lo = mid + 1;
mid = lo + (hi - lo) / 2;
}
return max(0, hi);
}
};
Input
matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output
true
#3 Code Example with Java Programming
Code -
Java Programming
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int rows = matrix.length;
int cols = matrix[0].length;
int rowIdx = rows - 1;
int colIdx = 0;
while (rowIdx >= 0 && colIdx < cols) {
if (matrix[rowIdx][colIdx] > target) {
rowIdx--;
} else if (matrix[rowIdx][colIdx] < target) {
colIdx++;
} else {
return true;
}
}
return false;
}
}
Input
matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output
false
#4 Code Example with Javascript Programming
Code -
Javascript Programming
const searchMatrix = function(matrix, target) {
if (matrix == null || matrix.length == 0) {
return false;
}
const length = matrix.length;
for (let i = 0; i < length; i++) {
const row = matrix.shift();
let left = 0,
right = row.length - 1;
while (left < = right) {
const mid = left + parseInt((right - left) / 2);
if (row[mid] == target) {
return true;
} else if (row[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
}
return false;
};
Input
matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output
false
#5 Code Example with Python Programming
Code -
Python Programming
class Solution:
def searchMatrix(self, matrix, target):
return any(target in row for row in matrix)
Input
matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output
true
#6 Code Example with C# Programming
Code -
C# Programming
namespace LeetCode
{
public class _0240_SearchA2DMatrixII
{
public bool SearchMatrix(int[,] matrix, int target)
{
var n = matrix.GetLength(0);
var i = 0;
var m = matrix.GetLength(1) - 1;
while (i < n && m >= 0)
{
var cmp = matrix[i, m].CompareTo(target);
if (cmp == 0) return true;
else if (cmp > 0) m--;
else i++;
}
return false;
}
}
}
Input
matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output
true