#304 Leetcode Range Sum Query 2D - Immutable Solution in C, C++, Java, JavaScript, Python, C# Leetcode

Algorithm

Problem Name: 304. Range Sum Query 2D - Immutable

Problem Link: https://leetcode.com/problems/range-sum-query-2d-immutable/

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

You must design an algorithm where sumRegion works on O(1) time complexity.

Example 1:

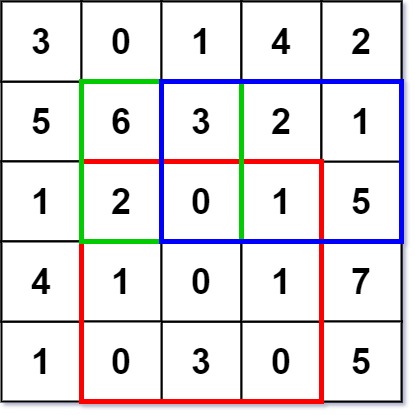
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-10⁴ <= matrix[i][j] <= 10⁴
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
At most 10⁴ calls will be made to sumRegion.

Code Examples

#1 Code Example with C++ Programming

Code - C++ Programming


class NumMatrix {
public:
    NumMatrix(vector<vector<int>> matrix) {
        for(int i = 0; i  <  matrix.size(); i++){
            dp.push_back(vector<int>());
            for(int j = 0; j  <  matrix[0].size(); j++)
                if(i == 0)
                    if(j == 0) dp[i].push_back(matrix[0][0]);
                    else dp[i].push_back(matrix[0][j] + dp[0][j - 1]);
                else
                    if(j == 0) dp[i].push_back(matrix[i][j] + dp[i - 1][0]);
                    else dp[i].push_back(matrix[i][j] + dp[i][j - 1] + dp[i - 1][j] - dp[i - 1][j - 1]);
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        int a = (row1 == 0) ? 0 : dp[row1 - 1][col2];
        int b = (col1 == 0) ? 0 : dp[row2][col1 - 1];
        int c = (row1 == 0 || col1 == 0) ? 0 : dp[row1 - 1][col1 - 1];
        return dp[row2][col2] - a - b + c;
    }
    
private:
    vector < vector<int>>dp;
};

Copy The Code & Try With Live Editor

Input

–

cmd

["NumMatrix", "sumRegion", "sumRegion", "sumRegion"] [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]

Output

–

cmd

[null, 8, 11, 12]

#2 Code Example with Java Programming

Code - Java Programming


class NumMatrix {

  int rows;
  int cols;
  int[][] rowLevelSum;
  public NumMatrix(int[][] matrix) {
    this.rows = matrix.length;
    this.cols = matrix[0].length;
    this.rowLevelSum = new int[rows][cols];
    for (int i = 0; i  <  rows; i++) {
      int sum = 0;
      for (int j = 0; j  <  cols; j++) {
        sum += matrix[i][j];
        this.rowLevelSum[i][j] = sum;
      }
    }
  }

  public int sumRegion(int row1, int col1, int row2, int col2) {
    int sum = 0;
    for (int i = row1; i  < = row2; i++) {
      sum += rowLevelSum[i][col2];
      if (col1 > 0) {
        sum -= rowLevelSum[i][col1 - 1];
      }
    }
    return sum;
  }
}

Copy The Code & Try With Live Editor

Input

–

cmd

["NumMatrix", "sumRegion", "sumRegion", "sumRegion"] [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]

Output

–

cmd

[null, 8, 11, 12]

#3 Code Example with Javascript Programming

Code - Javascript Programming


const NumMatrix = function(matrix) {
  const dp = [];
  if (matrix.length == 0 || matrix[0].length == 0) return;
  for (let i = 0; i  < = matrix.length; i++) {
    let t = new Array(matrix[0].length + 1).fill(0);
    dp.push(t);
  }

  for (let i = 0; i  <  matrix.length; i++) {
    for (let j = 0; j  <  matrix[0].length; j++) {
      dp[i + 1][j + 1] = dp[i][j + 1] + dp[i + 1][j] + matrix[i][j] - dp[i][j];
    }
  }

  this.cache = dp;
};

NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
  const dp = this.cache;
  return (
    dp[row2 + 1][col2 + 1] -
    dp[row1][col2 + 1] -
    dp[row2 + 1][col1] +
    dp[row1][col1]
  );
};

Copy The Code & Try With Live Editor

Input

–

cmd

["NumMatrix", "sumRegion", "sumRegion", "sumRegion"] [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]

Output

–

cmd

[null, 8, 11, 12]

#4 Code Example with Python Programming

Code - Python Programming


class NumMatrix:

    def __init__(self, matrix):
        self.sums = [[0] * (len(matrix and matrix[0]) + 1) for _ in range(len(matrix) + 1)]
        for i in range(len(matrix)):
            for j in range(len(matrix and matrix[0])):
                self.sums[i + 1][j + 1] = self.sums[i][j + 1] + self.sums[i + 1][j] - self.sums[i][j] + matrix[i][j]

    def sumRegion(self, row1, col1, row2, col2):
        return self.sums[row2 + 1][col2 + 1] - self.sums[row2 + 1][col1] - self.sums[row1][col2 + 1] + self.sums[row1][col1]

Copy The Code & Try With Live Editor

Input

–

cmd

["NumMatrix", "sumRegion", "sumRegion", "sumRegion"] [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]

Output

–

cmd

[null, 8, 11, 12]

Demonstration

Previous
#303 Leetcode Range Sum Query - Immutable Solution in C, C++, Java, JavaScript, Python, C# Leetcode

Next
#306 Leetcode Additive Number Solution in C, C++, Java, JavaScript, Python, C# Leetcode

Try With Live Editor

Category - Leetcode Online Judge Maniruzzaman Akash 1 year ago 359 0