Algorithm
Problem Name: 391. Perfect Rectangle
Given an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).
Return true if all the rectangles together form an exact cover of a rectangular region.
Example 1:
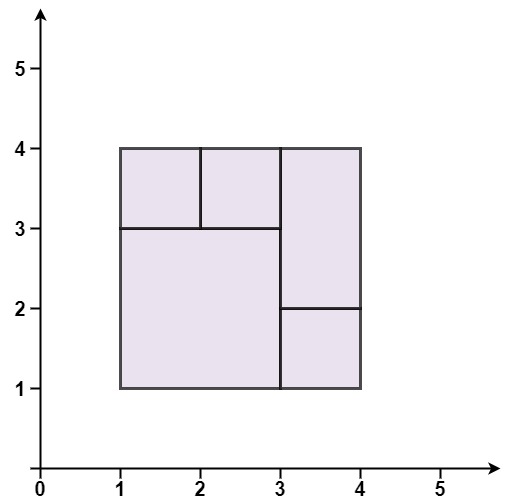
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]] Output: true Explanation: All 5 rectangles together form an exact cover of a rectangular region.
Example 2:
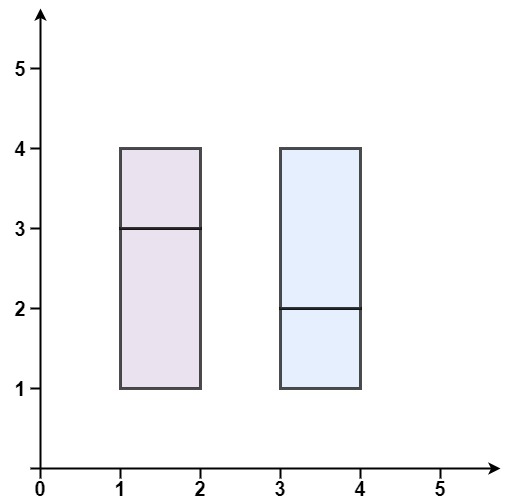
Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]] Output: false Explanation: Because there is a gap between the two rectangular regions.
Example 3:
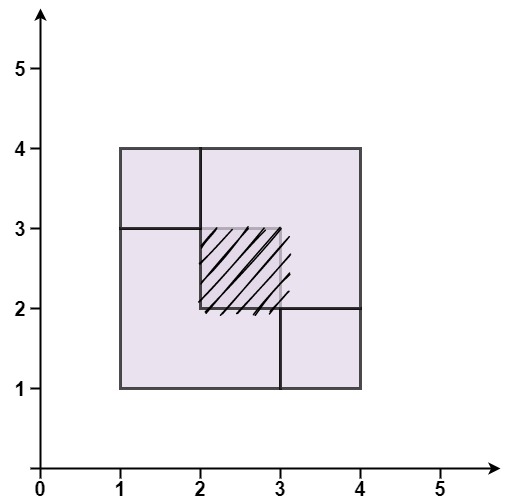
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]] Output: false Explanation: Because two of the rectangles overlap with each other.
Constraints:
1 <= rectangles.length <= 2 * 104rectangles[i].length == 4-105 <= xi, yi, ai, bi <= 105
Code Examples
#1 Code Example with C Programming
Code -
C Programming
typedef struct dot_s {
int x;
int y;
struct dot_s *shadow;
} dot_t;
#define HSZ 1000
typedef struct set_s {
dot_t **d;
int n;
} set_t;
int lookup_remove(set_t *set, int x, int y) {
dot_t **p, *d;
p = &set->d[x % HSZ];
while ((*p) && ((*p)->x != x || (*p)->y != y)) {
p = &((*p)->shadow);
}
if (*p) {
d = *p;
*p = d->shadow;
free(d);
set->n --;
return 1;
}
return 0;
}
void add2set(set_t *set, int x, int y) {
dot_t *d = malloc(sizeof(dot_t));
//assert(d);
d->x = x;
d->y = y;
d->shadow = set->d[x % HSZ];
set->d[x % HSZ] = d;
set->n ++;
}
bool map_area(int **rectangles, int rowsz) {
int a, i;
int x1, y1, x2, y2;
int x_min, y_min, x_max, y_max;
dot_t *buff[HSZ * 2] = { 0 };
set_t set = { 0 };
set.d = &buff[HSZ];
a = 0;
for (i = 0; i < rowsz; i ++) {
x1 = rectangles[i][0];
y1 = rectangles[i][1];
x2 = rectangles[i][2];
y2 = rectangles[i][3];
a += (x2 - x1) * (y2 - y1); // total area
if (i == 0 || x_min > x1) x_min = x1; // find the outermost shape
if (i == 0 || y_min > y1) y_min = y1;
if (i == 0 || x_max < x2) x_max = x2;
if (i == 0 || y_max < y2) y_max = y2;
if (!lookup_remove(&set, x1, y1)) add2set(&set, x1, y1);
if (!lookup_remove(&set, x1, y2)) add2set(&set, x1, y2);
if (!lookup_remove(&set, x2, y1)) add2set(&set, x2, y1);
if (!lookup_remove(&set, x2, y2)) add2set(&set, x2, y2);
}
return ((a == ((y_max - y_min) * (x_max - x_min))) &&
(set.n == 4 &&
lookup_remove(&set, x_min, y_min) &&
lookup_remove(&set, x_min, y_max) &&
lookup_remove(&set, x_max, y_min) &&
lookup_remove(&set, x_max, y_max))) ? true : false;
}
bool isRectangleCover(int** rectangles, int rectanglesRowSize, int rectanglesColSize) {
Input
rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
Output
true
#2 Code Example with Java Programming
Code -
Java Programming
class Solution {
public boolean isRectangleCover(int[][] rectangles) {
int x1 = Integer.MAX_VALUE;
int x2 = Integer.MIN_VALUE;
int y1 = Integer.MAX_VALUE;
int y2 = Integer.MIN_VALUE;
Set < String> set = new HashSet();
int totalArea = 0;
for (int[] rectangle : rectangles) {
x1 = Math.min(rectangle[0], x1);
y1 = Math.min(rectangle[1], y1);
x2 = Math.max(rectangle[2], x2);
y2 = Math.max(rectangle[3], y2);
totalArea += (rectangle[2] - rectangle[0]) * (rectangle[3] - rectangle[1]);
String s1 = rectangle[0] + " " + rectangle[1];
String s2 = rectangle[0] + " " + rectangle[3];
String s3 = rectangle[2] + " " + rectangle[3];
String s4 = rectangle[2] + " " + rectangle[1];
if (!set.add(s1)) {
set.remove(s1);
}
if (!set.add(s2)) {
set.remove(s2);
}
if (!set.add(s3)) {
set.remove(s3);
}
if (!set.add(s4)) {
set.remove(s4);
}
}
if (!set.contains(x1 + " " + y1) ||
!set.contains(x1 + " " + y2) ||
!set.contains(x2 + " " + y1) ||
!set.contains(x2 + " " + y2) ||
set.size() != 4) {
return false;
}
return totalArea == (x2 - x1) * (y2 - y1);
}
}
Input
rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
Output
true
#3 Code Example with Javascript Programming
Code -
Javascript Programming
const isRectangleCover = function(rectangles) {
let tls = new Set()
let trs = new Set()
let bls = new Set()
let brs = new Set()
let corner = (x, y) => `${x} ${y}`
for (let [l, b, r, t] of rectangles) {
let tl = corner(t, l)
let tr = corner(t, r)
let bl = corner(b, l)
let br = corner(b, r)
if (tls.has(tl) || trs.has(tr) || bls.has(bl) || brs.has(br)) return false
if (!bls.delete(tl) && !trs.delete(tl)) tls.add(tl)
if (!brs.delete(tr) && !tls.delete(tr)) trs.add(tr)
if (!brs.delete(bl) && !tls.delete(bl)) bls.add(bl)
if (!bls.delete(br) && !trs.delete(br)) brs.add(br)
}
return tls.size === 1 && trs.size === 1 && bls.size === 1 && brs.size === 1
}
Input
rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
Output
false
#4 Code Example with Python Programming
Code -
Python Programming
class Solution:
def isRectangleCover(self, rectangles):
cnt = collections.Counter()
for x1, y1, x2, y2 in rectangles:
cnt[(x1, y1)] += 1
cnt[(x1, y2)] += 1
cnt[(x2, y2)] += 1
cnt[(x2, y1)] += 1
x1, y1, x2, y2 = min([r[:2] for r in rectangles]) + max(r[-2:] for r in rectangles)
for x, y in ((x1, y1), (x1, y2), (x2, y2), (x2, y1)):
if cnt[(x, y)] != 1: return False
cnt.pop((x, y))
return all(cnt[k] in (2, 4) for k in cnt) and sum((x2 - x1) * (y2 - y1) for x1, y1, x2, y2 in rectangles) == (x2 - x1) * (y2 - y1)
Input
rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
Output
false