Algorithm
Problem Name: 463. Island Perimeter
You are given row x col grid representing a map where grid[i][j] = 1 represents land and grid[i][j] = 0 represents water.
Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
Example 1:
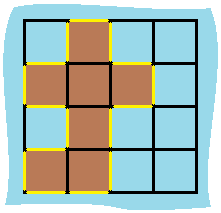
Input: grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]] Output: 16 Explanation: The perimeter is the 16 yellow stripes in the image above.
Example 2:
Input: grid = [[1]] Output: 4
Example 3:
Input: grid = [[1,0]] Output: 4
Constraints:
row == grid.lengthcol == grid[i].length1 <= row, col <= 100grid[i][j]is0or1.- There is exactly one island in
grid.
Code Examples
#1 Code Example with C Programming
Code -
C Programming
int islandPerimeter(int** grid, int gridRowSize, int gridColSize) {
int m = 0;
int i, j;
for (i = 0; i < gridRowSize; i ++) {
for (j = 0; j < gridColSize; j ++) {
if (grid[i][j] == 1) {
if (i == 0 || grid[i - 1][j] == 0) {
m ++;
}
if (i == gridRowSize - 1 || grid[i + 1][j] == 0) {
m ++;
}
if (j == 0 || grid[i][j - 1] == 0) {
m ++;
}
if (j == gridColSize - 1 || grid[i][j + 1] == 0) {
m ++;
}
}
}
}
return m;
}
Input
Output
#2 Code Example with Java Programming
Code -
Java Programming
class Solution {
int[][] dirs = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
public int islandPerimeter(int[][] grid) {
int sum = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {
for (int[] dir : dirs) {
sum += isBoundary(grid, i + dir[0], j + dir[1]) ? 1 : 0;
}
}
}
}
return sum;
}
private boolean isBoundary(int[][] grid, int x, int y) {
return x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] == 0;
}
}
Input
Output
#3 Code Example with Javascript Programming
Code -
Javascript Programming
const islandPerimeter = function(grid) {
let len = 0;
for (let r = 0; r < grid.length; r++) {
for (let c = 0; c < grid[0].length; c++) {
if (grid[r][c] === 1) {
len += cell(grid, r, c);
}
}
}
return len;
};
function cell(grid, r, c) {
let len = 0;
// top
if (r === 0 || grid[r - 1][c] !== 1) {
len += 1;
}
// left
if (c === 0 || grid[r][c - 1] !== 1) {
len += 1;
}
// right
if (grid[r][c + 1] !== 1) {
len += 1;
}
// bottom
if (grid[r + 1] == null || grid[r + 1][c] !== 1) {
len += 1;
}
return len;
}
console.log(
islandPerimeter([[0, 1, 0, 0], [1, 1, 1, 0], [0, 1, 0, 0], [1, 1, 0, 0]])
);
Input
Output
#4 Code Example with Python Programming
Code -
Python Programming
class Solution:
def islandPerimeter(self, grid: List[List[int]]) -> int:
self.res = 0
used = set()
def dfs(i, j):
used.add((i, j))
self.res += 4
for x, y in (i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1):
if 0 <= x < m and 0 <= y < n and grid[x][y]:
self.res -= 1
if (x, y) not in used:
dfs(x, y)
m, n = len(grid), len(grid[0])
for i in range(m):
for j in range(n):
if grid[i][j] == 1 and (i, j) not in used:
dfs(i, j)
return self.res
Input
Output
#5 Code Example with C# Programming
Code -
C# Programming
namespace LeetCode
{
public class _0463_IslandPerimeter
{
public int IslandPerimeter(int[][] grid)
{
var result = 0;
var row = grid.Length;
var col = grid[0].Length;
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
{
if (grid[i][j] == 1)
{
result += 4;
if (i > 0 && grid[i - 1][j] == 1)
result -= 2;
if (j > 0 && grid[i][j - 1] == 1)
result -= 2;
}
}
return result;
}
}
}
Input
Output
