Algorithm
Problem Name: 935. Knight Dialer
The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
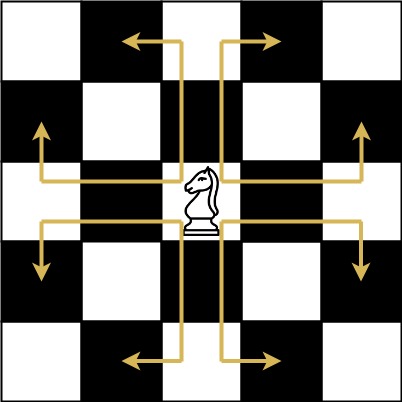
We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).
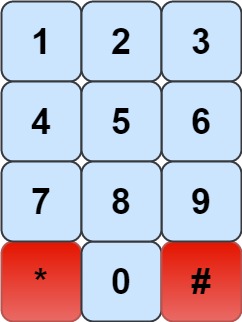
Given an integer n, return how many distinct phone numbers of length n we can dial.
You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.
As the answer may be very large, return the answer modulo 109 + 7.
Example 1:
Input: n = 1 Output: 10 Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
Example 2:
Input: n = 2 Output: 20 Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]
Example 3:
Input: n = 3131 Output: 136006598 Explanation: Please take care of the mod.
Constraints:
1 <= n <= 5000
Code Examples
#1 Code Example with C Programming
Code -
C Programming
#define MOD 1000000007
const int map[][4] = {
/* 0 */ { 4, 6, -1 },
/* 1 */ { 6, 8, -1 },
/* 2 */ { 7, 9, -1 },
/* 3 */ { 4, 8, -1 },
/* 4 */ { 3, 9, 0, -1 },
/* 5 */ { -1 },
/* 6 */ { 1, 7, 0, -1 },
/* 7 */ { 2, 6, -1 },
/* 8 */ { 1, 3, -1 },
/* 9 */ { 2, 4, -1 }
};
/* simple back tracking, need to add memorization to pass TLE */
#if 0
int helper(int p, int n) {
int *m, s, steps = 0;
if (n == 0) return 1;
if (p == 5) return -1;
m = map[p];
while (*m != -1) {
s = helper(*m, n - 1);
if (s > 0) steps += s;
m ++;
}
return steps;
}
#endif
int knightDialer(int N) {
int buff[20] = { 0 };
int *p, *n, *t, i, k = 0;
p = buff;
n = &buff[10];
p[0] = p[1] = p[2] = p[3] = p[4] =
p[5] = p[6] = p[7] = p[8] = p[9] = 1;
if (N > 1) p[5] = 0;
while (N -- > 1) {
n[0] = (p[4] + p[6]) % MOD;
n[1] = (p[6] + p[8]) % MOD;
n[2] = (p[7] + p[9]) % MOD;
n[3] = (p[4] + p[8]) % MOD;
n[4] = ((p[3] + p[9]) % MOD + p[0]) % MOD;
n[6] = ((p[1] + p[7]) % MOD + p[0]) % MOD;
n[7] = (p[2] + p[6]) % MOD;
n[8] = (p[1] + p[3]) % MOD;
n[9] = (p[2] + p[4]) % MOD;
t = p;
p = n;
n = t;
}
for (i = 0; i < 10; i ++) {
k = (k + p[i]) % MOD;
}
return k;
}
Input
Output
#2 Code Example with C++ Programming
Code -
C++ Programming
class Solution {
public:
int knightDialer(int N) {
vector<long>dp(10, 1);
vector < long>next(10, 1);
vector<int>ways(10, 2); // Number of ways we can jump from position X
ways[5] = 0;
ways[4] = 3;
ways[6] = 3;
long res = 10;
while (--N) {
res = 0;
for (auto& x: dp) {
x %= 1000000007;
}
for (int j = 0; j < 10; ++j) {
res += dp[j] * ways[j];
res %= 1000000007;
}
next[1] = dp[6] + dp[8];
next[2] = dp[7] + dp[9];
next[3] = dp[4] + dp[8];
next[4] = dp[3] + dp[9] + dp[0];
next[6] = dp[1] + dp[7] + dp[0];
next[7] = dp[2] + dp[6];
next[8] = dp[1] + dp[3];
next[9] = dp[2] + dp[4];
next[0] = dp[4] + dp[6];
swap(dp, next);
}
return res;
}
};
Input
Output
#3 Code Example with Java Programming
Code -
Java Programming
class Solution {
public static final int max = (int) Math.pow(10, 9) + 7;
public int knightDialer(int n) {
// A 3D array to store the solutions to the subproblems
long M[][][] = new long[n + 1][4][3];
long s = 0;
//do n hops from every i, j index (the very requirement of the problem)
for(int i = 0; i < 4; i++) {
for(int j = 0; j < 3; j++) {
s = (s + paths(M, i, j, n)) % max;
}
}
return (int) s;
}
private long paths(long[][][] M, int i, int j, int n) {
// if the knight hops outside of the matrix or to * return 0
//as there are no unique paths from here
if(i < 0 || j < 0 || i >= 4 || j >= 3 || (i == 3 && j != 1)) {
return 0;
}
if(n == 1) {
return 1;
}
//if the subproblem's solution is already computed, then return it
if(M[n][i][j] > 0) {
return M[n][i][j];
}
//else compute the subproblem's solution and save it in memory
M[n][i][j] = paths(M, i - 1, j - 2, n - 1) % max + // jump to a
paths(M, i - 2, j - 1, n - 1) % max + // jump to b
paths(M, i - 2, j + 1, n - 1) % max + // jump to c
paths(M, i - 1, j + 2, n - 1) % max + // jump to d
paths(M, i + 1, j + 2, n - 1) % max + // jump to e
paths(M, i + 2, j + 1, n - 1) % max + // jump to f
paths(M, i + 2, j - 1, n - 1) % max + // jump to g
paths(M, i + 1, j - 2, n - 1) % max; // jump to h
return M[n][i][j];
}
}
Input
Output
#4 Code Example with Python Programming
Code -
Python Programming
class Solution:
def knightDialer(self, N):
x1 = x2 = x3 = x4 = x5 = x6 = x7 = x8 = x9 = x0 = 1
for _ in range(N - 1):
x1, x2, x3, x4, x5, x6, x7, x8, x9, x0 = \u005C
x6 + x8, x7 + x9, x4 + x8, \u005C
x7 + x9 + x0, 0, x1 + x7 + x0, \u005C
x2 + x6, x1 + x7, x2 + x4, \u005C
x4 + x6
return (x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x0) % (10 ** 9 + 7)
Input
Output
