Algorithm
Problem Name: 655. Print Binary Tree
Given the root of a binary tree, construct a 0-indexed m x n string matrix res that represents a formatted layout of the tree. The formatted layout matrix should be constructed using the following rules:
- The height of the tree is
heightand the number of rowsmshould be equal toheight + 1. - The number of columns
nshould be equal to2height+1 - 1. - Place the root node in the middle of the top row (more formally, at location
res[0][(n-1)/2]). - For each node that has been placed in the matrix at position
res[r][c], place its left child atres[r+1][c-2height-r-1]and its right child atres[r+1][c+2height-r-1]. - Continue this process until all the nodes in the tree have been placed.
- Any empty cells should contain the empty string
"".
Return the constructed matrix res.
Example 1:
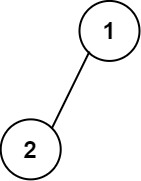
Input: root = [1,2] Output: [["","1",""], ["2","",""]]
Example 2:
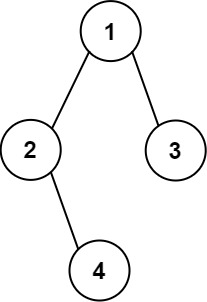
Input: root = [1,2,3,null,4] Output: [["","","","1","","",""], ["","2","","","","3",""], ["","","4","","","",""]]
Constraints:
- The number of nodes in the tree is in the range
[1, 210]. -99 <= Node.val <= 99- The depth of the tree will be in the range
[1, 10].
Code Examples
#1 Code Example with Java Programming
Code -
Java Programming
class Solution {
public List();
for (int i = 0; i < height; i++) {
List temp = new ArrayList<>();
for (int j = 0; j < numOfNodes; j++) {
temp.add("");
}
ans.add(temp);
}
updateList(ans, root, 0, 0, numOfNodes);
return ans;
}
private void updateList (List < List Input
root = [1,2]
Output
[["","1",""],
["2","",""]]
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const printTree = function (root) {
const h = getH(root)
const w = Math.pow(2, h) - 1
const matrix = new Array(h).fill(0).map((_) => new Array(w).fill(''))
fill(root, 0, 0, w - 1)
return matrix
function getH(root) {
if (!root) return 0
return Math.max(getH(root.left), getH(root.right)) + 1
}
function fill(root, level, start, end) {
if (!root) return
let mid = (start + end) / 2
matrix[level][mid] = root.val + ''
fill(root.left, level + 1, start, mid - 1)
fill(root.right, level + 1, mid + 1, end)
}
}
Input
root = [1,2]
Output
[["","1",""],
["2","",""]]
#3 Code Example with Python Programming
Code -
Python Programming
class Solution:
def printTree(self, root):
"""
:type root: TreeNode
:rtype: List[List[str]]
"""
def traverse(node):
if not node: return 0
return max(traverse(node.left), traverse(node.right)) * 2 + 1
length = traverse(root)
stack, dic, res, padding = [root], {root : length // 2}, [], length // 2
while any(stack):
out, tmp, padding = [""] * length, [], padding // 2
for i, node in enumerate(stack):
out[dic[node]] = str(node.val)
if node.left:
dic[node.left] = dic[node] - padding - 1
tmp.append(node.left)
if node.right:
dic[node.right] = dic[node] + padding + 1
tmp.append(node.right)
res.append(out)
stack = tmp
return res
Input
root = [1,2,3,null,4]
Output
[["","","","1","","",""],
["","2","","","","3",""],
["","","4","","","",""]]