Algorithm
Problem Name: 508. Most Frequent Subtree Sum
Problem Link: https://leetcode.com/problems/most-frequent-subtree-sum/
Given the root of a binary tree, return the most frequent subtree sum. If there is a tie, return all the values with the highest frequency in any order.
The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).
Example 1:
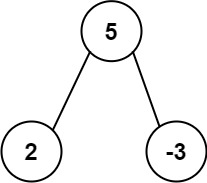
Input: root = [5,2,-3] Output: [2,-3,4]
Example 2:
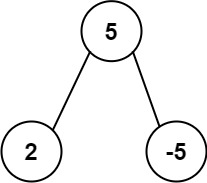
Input: root = [5,2,-5] Output: [2]
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. -105 <= Node.val <= 105
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
class Solution {
public:
vector<int> findFrequentTreeSum(TreeNode* root) {
vector<int>res;
unordered_map < int, int>m;
DFS(root, m);
int maxFreq = 0;
for(auto x: m)
if(x.second > maxFreq) res.clear(), res.push_back(x.first), maxFreq = x.second;
else if(x.second == maxFreq) res.push_back(x.first);
return res;
}
int DFS(TreeNode* root, unordered_map < int, int>& m){
if(!root) return 0;
int l = DFS(root->left, m);
int r = DFS(root->right, m);
int sum = root->val + l + r;
m[sum]++;
return sum;
}
};
Input
root = [5,2,-3]
Output
[2,-3,4]
#2 Code Example with Java Programming
Code -
Java Programming
class Solution {
public int[] findFrequentTreeSum(TreeNode root) {
Map subtreeSumFrequency = new HashMap<>();
Map < TreeNode, Integer> nodeToSum = new HashMap<>();
dfsHelper(root, nodeToSum, subtreeSumFrequency);
int maxFrequency = subtreeSumFrequency.values().stream()
.max(Comparator.comparingInt(Integer::intValue)).orElseGet(() -> 0);
return subtreeSumFrequency
.keySet()
.stream()
.filter(e -> subtreeSumFrequency.get(e) == maxFrequency)
.collect(Collectors.toList())
.stream()
.mapToInt(Integer::intValue)
.toArray();
}
private int dfsHelper(TreeNode node, Map < TreeNode, Integer> nodeToSum,
Map subtreeSumFrequency) {
if (node == null) {
return 0;
}
if (nodeToSum.containsKey(node)) {
return nodeToSum.get(node);
}
int leftSubtreeSum = dfsHelper(node.left, nodeToSum, subtreeSumFrequency);
int rightSubtreeSum = dfsHelper(node.right, nodeToSum, subtreeSumFrequency);
nodeToSum.put(node, node.val + leftSubtreeSum + rightSubtreeSum);
subtreeSumFrequency
.put(nodeToSum.get(node), subtreeSumFrequency.getOrDefault(nodeToSum.get(node), 0) + 1);
return nodeToSum.get(node);
}
}
Input
root = [5,2,-3]
Output
[2,-3,4]
#3 Code Example with Javascript Programming
Code -
Javascript Programming
const findFrequentTreeSum = function(root) {
if (root == null) return [];
const valArr = [];
calc(root, valArr);
const hash = {};
valArr.forEach((el, idx) => {
if (hash.hasOwnProperty(el)) {
hash[el] += 1;
} else {
hash[el] = 1;
}
});
const arr = Object.entries(hash).sort((a, b) => b[1] - a[1]);
const max = arr[0][1];
const res = [+arr[0][0]];
for (let i = 1; i < arr.length; i++) {
if (arr[i][1] === max) {
res.push(+arr[i][0]);
} else {
return res;
}
}
return res;
};
function calc(node, arr) {
let sum = 0;
if (node.left) {
sum += calc(node.left, arr);
}
if (node.right) {
sum += calc(node.right, arr);
}
sum += node.val;
arr.push(sum);
return sum;
}
Input
root = [5,2,-5]
Output
[2]
#4 Code Example with C# Programming
Code -
C# Programming
class Solution:
def findFrequentTreeSum(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
if not root: return []
def traverse(node):
if not node: return 0
sm = traverse(node.left) + traverse(node.right) + node.val
if sm in dic: dic[sm] += 1
else: dic[sm] = 1
return sm
dic = {}
traverse(root)
mx = max(dic.values())
return [k for k in dic.keys() if dic[k] == mx]
Input
root = [5,2,-5]
Output
[2]