Algorithm
Problem Name: 1240. Tiling a Rectangle with the Fewest Squares
Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.
Example 1:
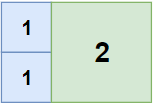
Input: n = 2, m = 3 Output: 3 Explanation:3squares are necessary to cover the rectangle.2(squares of1x1)1(square of2x2)
Example 2:
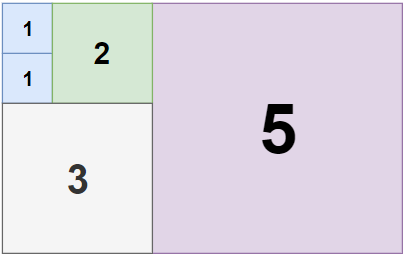
Input: n = 5, m = 8 Output: 5
Example 3:
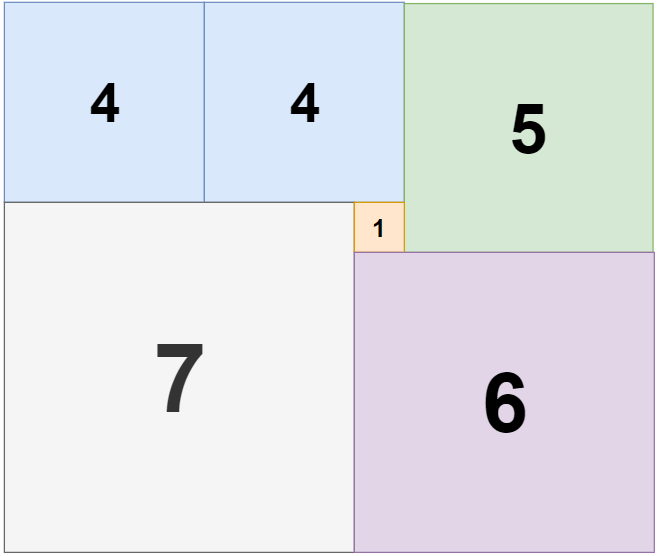
Input: n = 11, m = 13 Output: 6
Constraints:
1 <= n, m <= 13
Code Examples
#1 Code Example with Javascript Programming
Code -
Javascript Programming
const tilingRectangle = function (n, m) {
if ((n === 11 && m === 13) || (n === 13 && m === 11)) {
return 6
}
const dp = Array(n + 1)
.fill()
.map((_) => Array(m + 1).fill(0))
for (let i = 1; i < = n; i++) {
for (let j = 1; j < = m; j++) {
if (i === j) {
dp[i][j] = 1
continue
}
dp[i][j] = m * n
for (let k = 1; k < = i / 2; k++) {
dp[i][j] = Math.min(dp[i][j], dp[i - k][j] + dp[k][j])
}
for (let k = 1; k < = j / 2; k++) {
dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[i][j - k])
}
}
}
return dp[n][m]
}
Input
n = 2, m = 3
Output
3
#2 Code Example with Python Programming
Code -
Python Programming
class Solution:
memo = {}
def tilingRectangle(self, n: int, m: int) -> int:
if (n, m) in {(11, 13), (13, 11)}:
return 6
if n == m:
return 1
if (n, m) not in self.memo:
nMin = mMin = float("inf")
for i in range(1, n // 2 + 1):
nMin = min(
nMin, self.tilingRectangle(i, m) + self.tilingRectangle(n - i, m)
)
for j in range(1, m // 2 + 1):
mMin = min(
mMin, self.tilingRectangle(n, j) + self.tilingRectangle(n, m - j)
)
self.memo[(n, m)] = min(nMin, mMin)
return self.memo[(n, m)]
Input
n = 2, m = 3
Output
3
