Algorithm
Problem Name: 1091. Shortest Path in Binary Matrix
Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.
A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:
- All the visited cells of the path are
0. - All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).
The length of a clear path is the number of visited cells of this path.
Example 1:
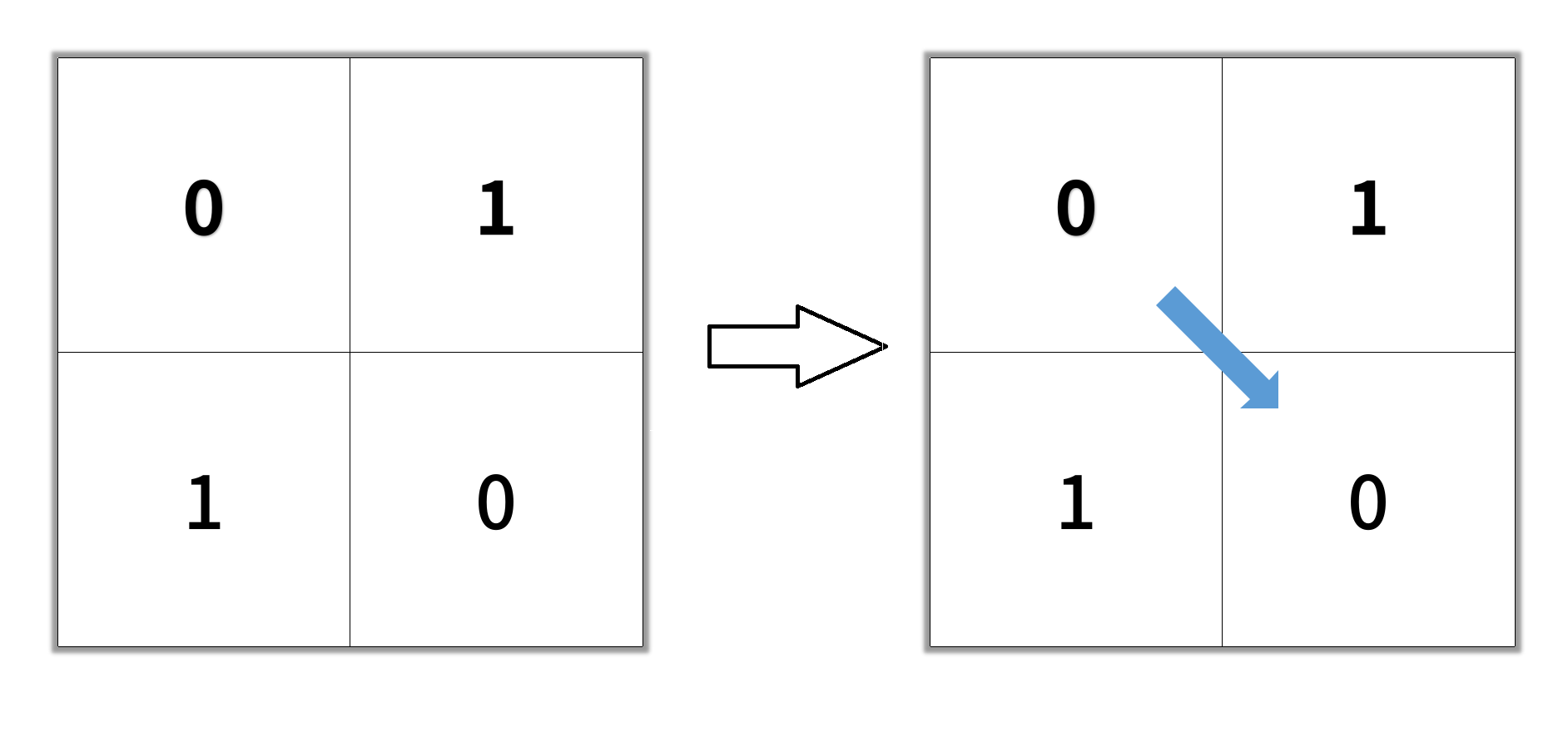
Input: grid = [[0,1],[1,0]] Output: 2
Example 2:
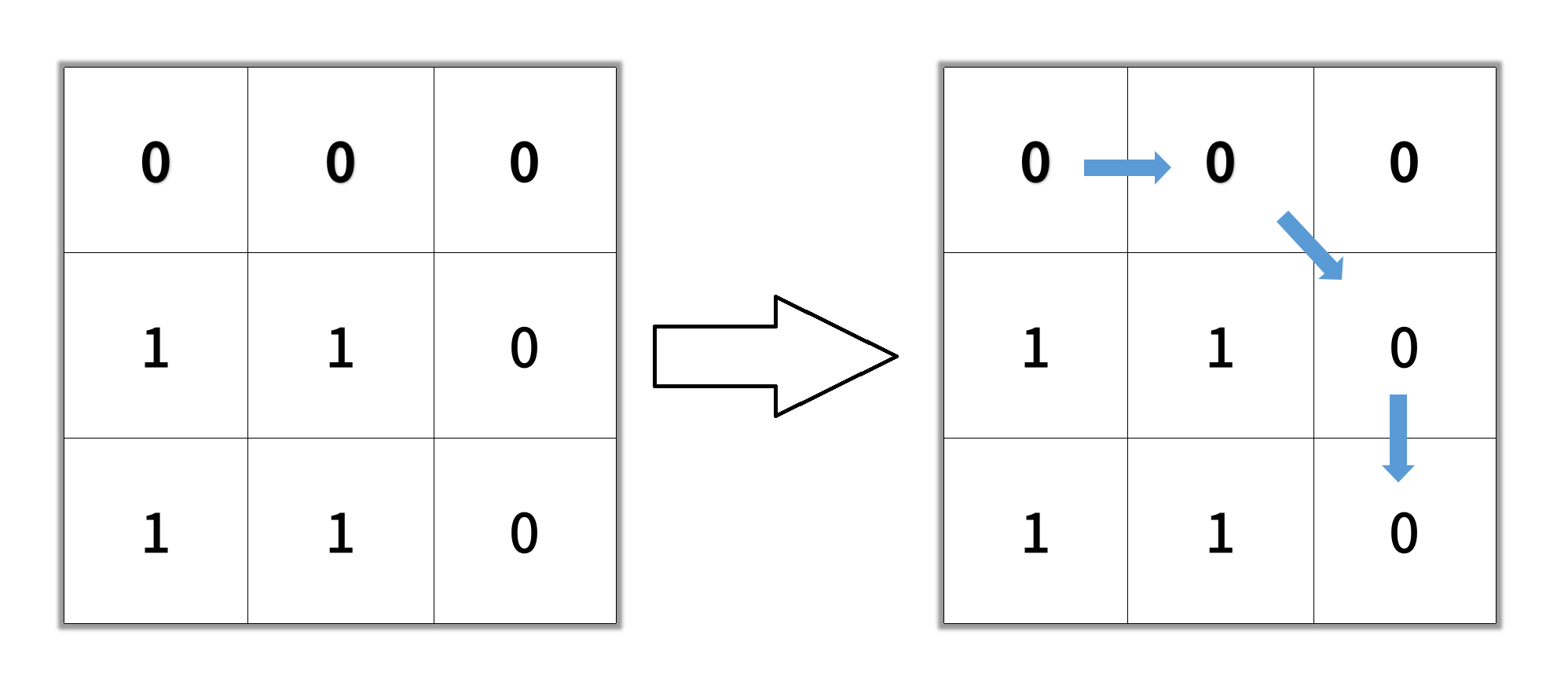
Input: grid = [[0,0,0],[1,1,0],[1,1,0]] Output: 4
Example 3:
Input: grid = [[1,0,0],[1,1,0],[1,1,0]] Output: -1
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 100grid[i][j] is 0 or 1
Code Examples
#1 Code Example with Java Programming
Code -
Java Programming
class Solution {
private final int[][] DIRS = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}, {1, 1}, {-1, 1}, {1, -1}, {-1, -1}};
public int shortestPathBinaryMatrix(int[][] grid) {
if (grid[0][0] == 1) {
return -1;
}
int numRows = grid.length;
int numCols = grid[0].length;
boolean[][] visited = new boolean[numRows][numCols];
Queue < int[]> queue = new LinkedList<>();
queue.add(new int[]{0, 0});
visited[0][0] = true;
int numOfSteps = 0;
while (!queue.isEmpty()) {
numOfSteps++;
int size = queue.size();
while (size-- > 0) {
int[] removed = queue.remove();
int x = removed[0];
int y = removed[1];
if (x == numRows - 1 && y == numCols - 1) {
return numOfSteps;
}
for (int[] dir : DIRS) {
int newX = x + dir[0];
int newY = y + dir[1];
if (newX >= 0 && newY >= 0 && newX < numRows && newY < numCols && !visited[newX][newY] && grid[newX][newY] == 0) {
queue.add(new int[]{newX, newY});
visited[newX][newY] = true;
}
}
}
}
return -1;
}
}
Input
grid = [[0,1],[1,0]]
Output
2
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const shortestPathBinaryMatrix = function(grid) {
if(grid == null || grid.length === 0 || grid[0][0] === 1) return -1
let res = 1
const n = grid.length
const dirs = [
[1, 0],
[-1, 0],
[0, 1],
[0, -1],
[-1, -1],
[-1, 1],
[1, 1],
[1, -1],
]
let q = [[0, 0]]
while(q.length) {
const tmp = q
q = []
for(let [x, y] of tmp) {
if (x < 0 || x >= n || y < 0 || y >= n || grid[x][y] !== 0) continue
if(x === n - 1 && y === n - 1) return res
grid[x][y] = 1
for(let [dx, dy] of dirs) {
q.push([x + dx, y + dy])
}
}
res++
}
return -1
};
Input
grid = [[0,1],[1,0]]
Output
2
#3 Code Example with Python Programming
Code -
Python Programming
class Solution:
def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
n = len(grid)
if grid[0][0] == 1:
return -1
bfs = [[0, 0]]
cnt = 1
seen = {(0, 0)}
while bfs:
new = []
for i, j in bfs:
for x, y in (i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1), (i - 1, j - 1), (i + 1, j + 1), (i - 1, j + 1), (i + 1, j - 1):
if 0 <= x < n and 0 <= y < n and (x, y) not in seen and not grid[x][y]:
if x == y == n - 1:
return cnt + 1
new.append((x, y))
seen.add((x, y))
cnt += 1
bfs = new
return -1
Input
grid = [[0,0,0],[1,1,0],[1,1,0]]
Output
4