Algorithm
Problem Name: 1123. Lowest Common Ancestor of Deepest Leaves
Given the root of a binary tree, return the lowest common ancestor of its deepest leaves.
Recall that:
- The node of a binary tree is a leaf if and only if it has no children
- The depth of the root of the tree is
0. if the depth of a node isd, the depth of each of its children isd + 1. - The lowest common ancestor of a set
Sof nodes, is the nodeAwith the largest depth such that every node inSis in the subtree with rootA.
Example 1:
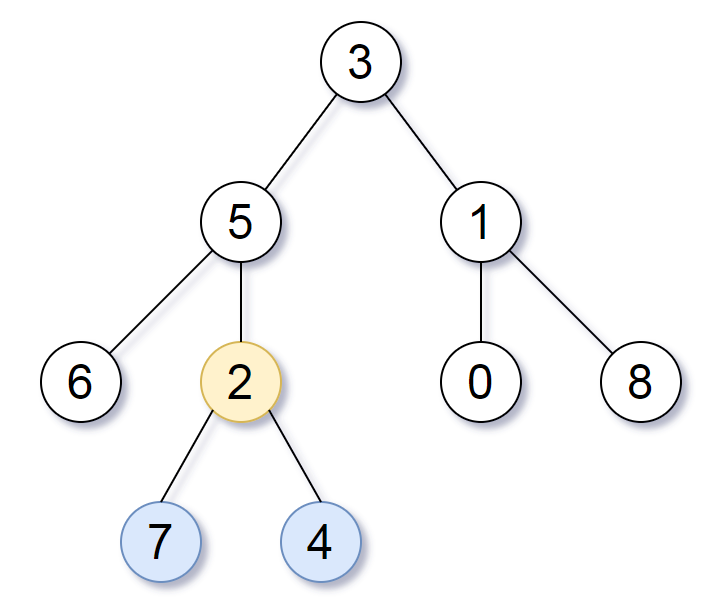
Input: root = [3,5,1,6,2,0,8,null,null,7,4] Output: [2,7,4] Explanation: We return the node with value 2, colored in yellow in the diagram. The nodes coloured in blue are the deepest leaf-nodes of the tree. Note that nodes 6, 0, and 8 are also leaf nodes, but the depth of them is 2, but the depth of nodes 7 and 4 is 3.
Example 2:
Input: root = [1] Output: [1] Explanation: The root is the deepest node in the tree, and it's the lca of itself.
Example 3:
Input: root = [0,1,3,null,2] Output: [2] Explanation: The deepest leaf node in the tree is 2, the lca of one node is itself.
Constraints:
- The number of nodes in the tree will be in the range
[1, 1000]. 0 <= Node.val <= 1000- The values of the nodes in the tree are unique.
Code Examples
#1 Code Example with Java Programming
Code -
Java Programming
class Solution {
public TreeNode lcaDeepestLeaves(TreeNode root) {
return dfs(root).node;
}
private NodeResult dfs(TreeNode root) {
if (root == null) {
return new NodeResult(null, 0);
}
NodeResult leftResult = dfs(root.left);
NodeResult rightResult = dfs(root.right);
if (leftResult.distance > rightResult.distance) {
return new NodeResult(leftResult.node, leftResult.distance + 1);
}
if (leftResult.distance < rightResult.distance) {
return new NodeResult(rightResult.node, rightResult.distance + 1);
}
return new NodeResult(root, rightResult.distance + 1);
}
private static class NodeResult {
TreeNode node;
int distance;
public NodeResult(TreeNode node, int distance) {
this.node = node;
this.distance = distance;
}
}
}
Input
root = [3,5,1,6,2,0,8,null,null,7,4]
Output
[2,7,4]
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const lcaDeepestLeaves = function(root) {
let maxDepth = 0, lcaNode = null
function lca(node, depth) {
if(node == null) return depth - 1
maxDepth = Math.max(depth, maxDepth)
const left = lca(node.left, depth + 1)
const right = lca(node.right, depth + 1)
if(left === maxDepth && right === maxDepth) {
lcaNode = node
}
return Math.max(left, right)
}
lca(root, 0)
return lcaNode
};
Input
root = [3,5,1,6,2,0,8,null,null,7,4]
Output
[2,7,4]
#3 Code Example with Python Programming
Code -
Python Programming
class Solution:
def lcaDeepestLeaves(self, root: TreeNode) -> TreeNode:
def helper(root):
if not root:
return 0, None
d1, lca1 = helper(root.left)
d2, lca2 = helper(root.right)
if d1 > d2:
node = lca1
elif d1 < d2:
node = lca2
else:
node = root
return max(d1, d2) + 1, node
return helper(root)[1]
Input
root = [1]
Output
[1]
#4 Code Example with C# Programming
Code -
C# Programming
using System;
namespace LeetCode
{
public class _1123_LowestCommonAncestorOfDeepestLeaves
{
private int maxDepth = 0;
private TreeNode result = null;
public TreeNode LcaDeepestLeaves(TreeNode root)
{
Helper(root, 0);
return result;
}
public int Helper(TreeNode node, int level)
{
if (node == null)
return 0;
int left = Helper(node.left, level + 1);
int right = Helper(node.right, level + 1);
if (left == right && level + left >= maxDepth)
{
maxDepth = level + left;
result = node;
}
return Math.Max(left, right) + 1;
}
}
}
Input
root = [1]
Output
[1]