Algorithm
Problem Name: 1222. Queens That Can Attack the King
On a 0-indexed 8 x 8 chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array queens where queens[i] = [xQueeni, yQueeni] represents the position of the ith black queen on the chessboard. You are also given an integer array king of length 2 where king = [xKing, yKing] represents the position of the white king.
Return the coordinates of the black queens that can directly attack the king. You may return the answer in any order.
Example 1:
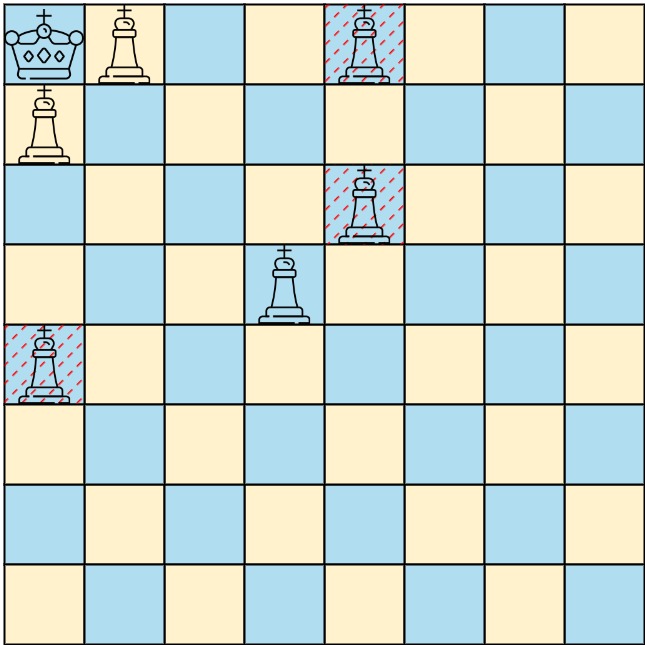
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0] Output: [[0,1],[1,0],[3,3]] Explanation: The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
Example 2:
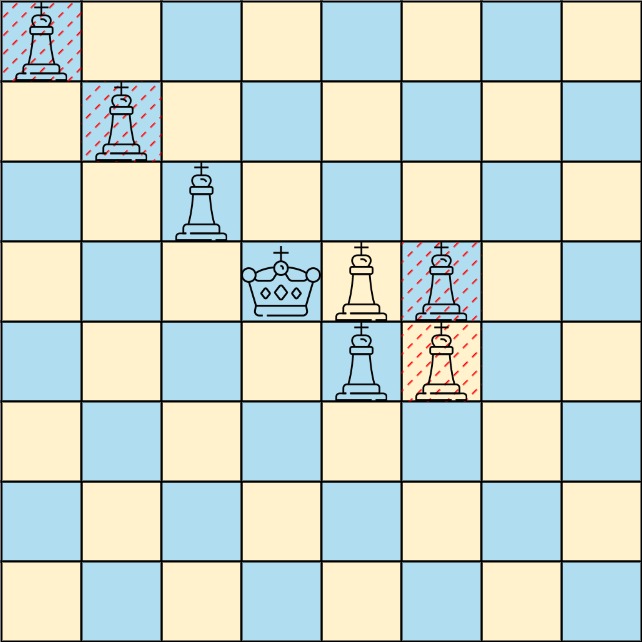
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3] Output: [[2,2],[3,4],[4,4]] Explanation: The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
Constraints:
1 <= queens.length < 64queens[i].length == king.length == 20 <= xQueeni, yQueeni, xKing, yKing < 8- All the given positions are unique.
Code Examples
#1 Code Example with Python Programming
Code -
Python Programming
class Solution:
def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:
def dfs(dr, dc, r, c):
while 0 <= r <= 7 and 0 <= c <= 7:
if (r, c) in q:
res.append([r, c])
break
r += dr
c += dc
q = set((r,c) for r, c in queens)
res = []
for dr, dc in (-1, -1), (-1, 0), (-1, 1), (0, 1), (1, 1), (1, 0), (1, -1), (0, -1):
dfs(dr, dc, *king)
return res
Input
queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output
[[0,1],[1,0],[3,3]]
#2 Code Example with C# Programming
Code -
C# Programming
using System.Collections.Generic;
using System.Linq;
namespace LeetCode
{
public class _1222_QueensThatCanAttackTheKing
{
public IList < IList<int>> QueensAttacktheKing(int[][] queens, int[] king)
{
var result = new List < IList<int>>();
var set = queens.Select(q => (q[0], q[1])).ToHashSet();
for (int r = -1; r < = 1; r++)
for (int c = -1; c < = 1; c++)
for (int length = 1; length < 8; length++)
{
var qc = king[1] + c * length;
var qr = king[0] + r * length;
if (qc < 0 || qc >= 8 || qr < 0 || qr >= 8) break;
if (set.Contains((qr, qc)))
{
result.Add(new int[] { qr, qc });
break;
}
}
return result;
}
}
}
Input
queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output
[[0,1],[1,0],[3,3]]