Algorithm
Problem Name: 375. Guess Number Higher or Lower II
We are playing the Guessing Game. The game will work as follows:
- I pick a number between
1andn. - You guess a number.
- If you guess the right number, you win the game.
- If you guess the wrong number, then I will tell you whether the number I picked is higher or lower, and you will continue guessing.
- Every time you guess a wrong number
x, you will payxdollars. If you run out of money, you lose the game.
Given a particular n, return the minimum amount of money you need to guarantee a win regardless of what number I pick.
Example 1:
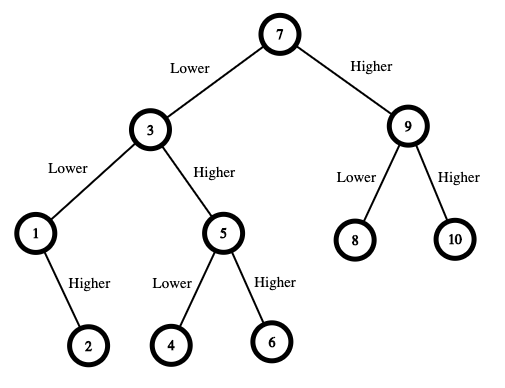
Input: n = 10 Output: 16 Explanation: The winning strategy is as follows: - The range is [1,10]. Guess 7. - If this is my number, your total is $0. Otherwise, you pay $7. - If my number is higher, the range is [8,10]. Guess 9. - If this is my number, your total is $7. Otherwise, you pay $9. - If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16. - If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16. - If my number is lower, the range is [1,6]. Guess 3. - If this is my number, your total is $7. Otherwise, you pay $3. - If my number is higher, the range is [4,6]. Guess 5. - If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5. - If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15. - If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15. - If my number is lower, the range is [1,2]. Guess 1. - If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1. - If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11. The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.
Example 2:
Input: n = 1 Output: 0 Explanation: There is only one possible number, so you can guess 1 and not have to pay anything.
Example 3:
Input: n = 2 Output: 1 Explanation: There are two possible numbers, 1 and 2. - Guess 1. - If this is my number, your total is $0. Otherwise, you pay $1. - If my number is higher, it must be 2. Guess 2. Your total is $1. The worst case is that you pay $1.
Constraints:
1 <= n <= 200
Code Examples
#1 Code Example with C Programming
Code -
C Programming
#define IDX(START, END, SZ) ((START - 1) * SZ + (END - 1))
int dp(int *p, int start, int end, int sz) {
int i, l, r, k, m;
if (start >= end) return 0;
m = p[IDX(start, end, sz)];
if (m) return m;
for (i = start; i < = end; i ++) {
k = i;
l = dp(p, start, i - 1, sz);
r = dp(p, i + 1, end, sz);
k += l > r ? l : r;
if (m == 0 || m > k) m = k;
}
p[IDX(start, end, sz)] = m;
return m;
}
int getMoneyAmount(int n) {
int *p = calloc(n * n, sizeof(int));
int m = dp(p, 1, n, n);
free(p);
return m;
}
Input
Output
#2 Code Example with Java Programming
Code -
Java Programming
class Solution {
public int getMoneyAmount(int n) {
int[][] dp = new int[n + 1][n + 1];
for (int i = 2; i < = n; i++) {
for (int j = 1; j < = n -i + 1; j++) {
int minres = Integer.MAX_VALUE;
for (int k = j; k < j + i - 1; k++) {
int res = k + Math.max(dp[j][k - 1], dp[k + 1][j + i - 1]);
minres = Math.min(minres, res);
}
dp[j][j + i - 1] = minres;
}
}
return dp[1][n];
}
}
Input
Output
#3 Code Example with Javascript Programming
Code -
Javascript Programming
const getMoneyAmount = function(n) {
const dp = Array.from({length: n + 1}, () => new Array(n + 1).fill(0))
return helper(dp, 1, n)
};
function helper(dp, s, e) {
if(s >= e) return 0
if(dp[s][e] !== 0) return dp[s][e]
let res = Number.MAX_VALUE
for(let i = s; i <= e; i++) {
const tmp = i + Math.max(helper(dp, s, i - 1), helper(dp, i + 1, e))
res = Math.min(res, tmp>
}
dp[s][e] = res
return res
}
Input
#4 Code Example with Python Programming
Code -
Python Programming
class Solution:
def getMoneyAmount(self, n):
dic = {}
def dfs(l, r):
if l >=r: return 0
if (l, r) not in dic: dic[(l, r)] = min(num + max(dfs(l, num - 1), dfs(num + 1, r)) for num in range(l, r))
return dic[(l, r)]
return dfs(1, n)
Input
#5 Code Example with C# Programming
Code -
C# Programming
using System;
namespace LeetCode
{
public class _0375_GuessNumberHigherOrLowerII
{
public int GetMoneyAmount(int n)
{
var dp = new int[n + 1, n + 1];
for (int len = 2; len < = n; len++)
for (int start = 1; start < = n - len + 1; start++)
{
var result = int.MaxValue;
for (int piv = start + (len - 1) / 2; piv < start + len - 1; piv++)
{
var value = piv + Math.Max(dp[start, piv - 1], dp[piv + 1, start + len - 1]);
result = Math.Min(result, value);
}
dp[start, start + len - 1] = result;
}
return dp[1, n];
}
}
}
Input
Output
