Algorithm
Problem Name: 1254. Number of Closed Islands
Problem Link: https://leetcode.com/problems/number-of-closed-islands/
Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.
Return the number of closed islands.
Example 1:
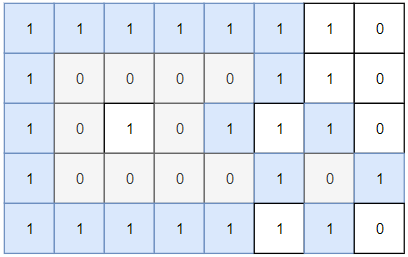
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]] Output: 2 Explanation: Islands in gray are closed because they are completely surrounded by water (group of 1s).
Example 2:
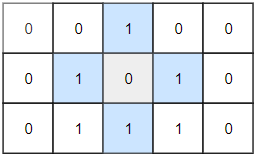
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]] Output: 1
Example 3:
Input: grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
Output: 2
Constraints:
1 <= grid.length, grid[0].length <= 1000 <= grid[i][j] <=1
Code Examples
#1 Code Example with Java Programming
Code -
Java Programming
class Solution {
private static final int[][] DIRS = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
public int closedIsland(int[][] grid) {
int closedIslandCount = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 0 && isSurroundedSuccessfully(grid, i, j)) {
closedIslandCount++;
}
}
}
return closedIslandCount;
}
private boolean isSurroundedSuccessfully(int[][] grid, int i, int j) {
Queue < int[]> queue = new LinkedList<>();
queue.add(new int[]{i, j});
boolean surroundingCheck = true;
while (!queue.isEmpty()) {
int[] removed = queue.remove();
int x = removed[0];
int y = removed[1];
if (x < 0 || y < 0 || x >= grid.length || y >= grid[0].length) {
surroundingCheck = false;
continue;
}
if (grid[x][y] == 1) {
continue;
}
grid[x][y] = 1;
for (int[] dir : DIRS) {
int newX = x + dir[0];
int newY = y + dir[1];
queue.add(new int[]{newX, newY});
}
}
return surroundingCheck;
}
}
Input
grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output
2
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const closedIsland = function(grid) {
const m = grid.length, n = grid[0].length
const dirs = [[0,1], [0,-1], [1,0], [-1,0]]
for(let i = 0; i < m; i++) {
for(let j = 0; j < n; j++) {
if((i=== 0 || i === m - 1 || j === 0 || j === n - 1) && grid[i][j] === 0){
fill(i, j)
}
}
}
let res = 0
for(let i = 0; i < m; i++) {
for(let j = 0; j < n; j++) {
if(grid[i][j] === 0) {
res++
fill(i, j)
}
}
}
return res
function fill(i, j> {
if(i < 0 || i >= m || j < 0 || j >= n || grid[i][j] !== 0) return
grid[i][j] = 1
for(const [dx, dy] of dirs) {
const nx = i + dx, ny = j + dy
fill(nx, ny)
}
}
};
Input
grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output
2
#3 Code Example with Python Programming
Code -
Python Programming
class Solution:
def closedIsland(self, grid: List[List[int]]) -> int:
def dfs(i, j, ret=True):
grid[i][j] = -1
for x, y in (i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1):
if 0 <= x < m and 0 <= y < n:
if not grid[x][y]:
ret &= dfs(x, y)
else:
ret = False
return ret
m, n = len(grid), len(grid[0])
return sum(dfs(i, j) for i in range(m) for j in range(n) if grid[i][j] == 0)
Input
grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output
1
#4 Code Example with C# Programming
Code -
C# Programming
namespace LeetCode
{
public class _1254_NumberOfClosedIslands
{
public int ClosedIsland(int[][] grid)
{
var N = grid.Length;
var M = grid[0].Length;
var uf = new UnionFind(grid);
for (int i = 0; i < N; i++)
for (int j = 0; j < M; j++)
if (grid[i][j] == 0)
{
if (i == 0 || j == 0 || i == N - 1 || j == M - 1)
uf.Union(i * M + j, N * M);
if (i - 1 >= 0 && grid[i - 1][j] == 0)
uf.Union(i * M + j, (i - 1) * M + j);
if (i + 1 < N && grid[i + 1][j] == 0)
uf.Union(i * M + j, (i + 1) * M + j);
if (j - 1 >= 0 && grid[i][j - 1] == 0)
uf.Union(i * M + j, i * M + j - 1);
if (j + 1 < M && grid[i][j + 1] == 0)
uf.Union(i * M + j, i * M + j + 1);
}
return uf.Count() - 1;
}
public class UnionFind
{
private int count = 0;
private int[] parents;
private int[] ranks;
public UnionFind(int[][] grid)
{
count = 0;
int N = grid.Length;
int M = grid[0].Length;
parents = new int[N * M + 1];
ranks = new int[N * M + 1];
for (int i = 0; i < N; i++)
for (int j = 0; j < M; j++)
{
if (grid[i][j] == 0)
{
parents[i * M + j] = i * M + j;
count++;
}
}
parents[N * M] = N * M;
count++;
}
public int Find(int index)
{
if (parents[index] != index)
parents[index] = Find(parents[index]);
return parents[index];
}
public void Union(int index1, int index2)
{
var pIndex1 = Find(index1);
var pIndex2 = Find(index2);
if (pIndex1 != pIndex2)
{
if (ranks[pIndex1] >= ranks[pIndex2])
{
parents[pIndex2] = pIndex1;
ranks[pIndex1]++;
}
else
{
parents[pIndex1] = pIndex2;
ranks[pIndex2]++;
}
count--;
}
}
public int Count()
{
return count;
}
}
}
}
Input
grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output
1