Algorithm
Problem Name: 756. Pyramid Transition Matrix
You are stacking blocks to form a pyramid. Each block has a color, which is represented by a single letter. Each row of blocks contains one less block than the row beneath it and is centered on top.
To make the pyramid aesthetically pleasing, there are only specific triangular patterns that are allowed. A triangular pattern consists of a single block stacked on top of two blocks. The patterns are given as a list of three-letter strings allowed, where the first two characters of a pattern represent the left and right bottom blocks respectively, and the third character is the top block.
- For example,
"ABC"represents a triangular pattern with a'C'block stacked on top of an'A'(left) and'B'(right) block. Note that this is different from"BAC"where'B'is on the left bottom and'A'is on the right bottom.
You start with a bottom row of blocks bottom, given as a single string, that you must use as the base of the pyramid.
Given bottom and allowed, return true if you can build the pyramid all the way to the top such that every triangular pattern in the pyramid is in allowed, or false otherwise.
Example 1:
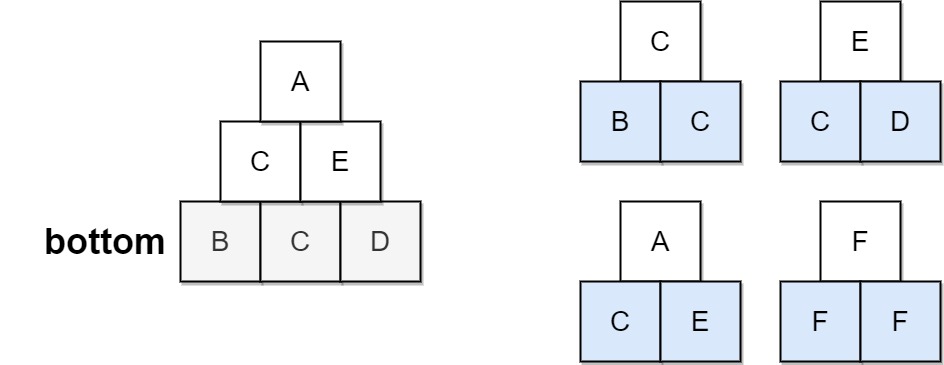
Input: bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"] Output: true Explanation: The allowed triangular patterns are shown on the right. Starting from the bottom (level 3), we can build "CE" on level 2 and then build "A" on level 1. There are three triangular patterns in the pyramid, which are "BCC", "CDE", and "CEA". All are allowed.
Example 2:
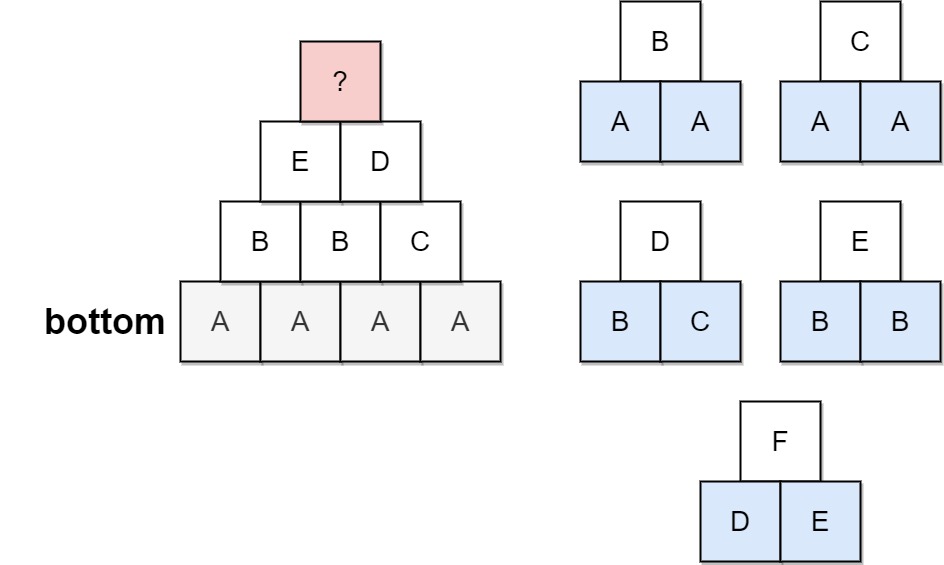
Input: bottom = "AAAA", allowed = ["AAB","AAC","BCD","BBE","DEF"] Output: false Explanation: The allowed triangular patterns are shown on the right. Starting from the bottom (level 4), there are multiple ways to build level 3, but trying all the possibilites, you will get always stuck before building level 1.
Constraints:
2 <= bottom.length <= 60 <= allowed.length <= 216allowed[i].length == 3- The letters in all input strings are from the set
{'A', 'B', 'C', 'D', 'E', 'F'}. - All the values of
allowedare unique.
Code Examples
#1 Code Example with Javascript Programming
Code -
Javascript Programming
const pyramidTransition = function (bottom, allowed) {
const m = new Map()
for (let e of allowed) {
const p = e.slice(0, 2)
if (!m.has(p)) m.set(p, new Set())
m.get(p).add(e[2])
}
return dfs(bottom, '', m, 0)
}
function dfs(row, next, m, i) {
if (row.length === 1) return true
if (next.length + 1 === row.length) return dfs(next, '', m, 0)
for (let c of m.get(row.slice(i, i + 2)) || new Set())
if (dfs(row, next + c, m, i + 1)) return true
return false
}
Input
Output
#2 Code Example with Python Programming
Code -
Python Programming
class Solution:
def pyramidTransition(self, bottom, allowed):
chars, allowed = 'ABCDEFG', set(allowed)
def dfs(r, q, i):
if len(r) == 1:
return True
for c in chars:
if r[i:i+2]+c in allowed and (i==len(r)-2 and dfs(q+c,"",0) or dfs(r,q+c,i+1)): return True
return False
return dfs(bottom, "", 0)
Input
Output
