Algorithm
Problem Name: 785. Is Graph Bipartite?
There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:
- There are no self-edges (
graph[u]does not containu). - There are no parallel edges (
graph[u]does not contain duplicate values). - If
vis ingraph[u], thenuis ingraph[v](the graph is undirected). - The graph may not be connected, meaning there may be two nodes
uandvsuch that there is no path between them.
A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.
Return true if and only if it is bipartite.
Example 1:
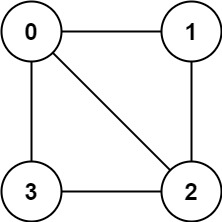
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]] Output: false Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
Constraints:
graph.length == n1 <= n <= 1000 <= graph[u].length < n0 <= graph[u][i] <= n - 1graph[u]does not containu.- All the values of
graph[u]are unique. - If
graph[u]containsv, thengraph[v]containsu.
Code Examples
#1 Code Example with C++ Programming
Code -
C++ Programming
class Solution {
public:
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
vector<int>color(n);
color[0] = 1;
for(int i = 0; i < n; i++){
auto neigh = graph[i];
if(!color[i]) for(auto j: neigh) if(color[j]){ color[i] = -color[j]; break; } // If un-colored, pick a color by neighbor
if(!color[i]) color[i] = 1; // Empty neighbor or no colored neighbor, colored 1 as default
for(auto j: neigh)
if(!color[j]) color[j] = -color[i];
else if(color[i] != -color[j]) return false;
}
return true;
}
};
Input
Output
#2 Code Example with Java Programming
Code -
Java Programming
class Solution {
public boolean isBipartite(int[][] graph) {
int n = graph.length;
int[] color = new int[n];
Arrays.fill(color, -1);
for (int i = 0; i < n; i++) {
if (color[i] == -1 && !bipartiteCheck(graph, i, color)) {
return false;
}
}
return true;
}
private boolean bipartiteCheck(int[][] graph, int node, int[] color) {
Queue < Integer> queue = new LinkedList<>();
queue.add(node);
int currColor = 0;
while (!queue.isEmpty()) {
int size = queue.size();
while (size-- > 0) {
int removed = queue.remove();
if (color[removed] != -1) {
if (color[removed] != currColor) {
return false;
}
continue;
}
color[removed] = currColor;
for (int conn : graph[removed]) {
if (color[conn] == -1) {
queue.add(conn);
}
}
}
currColor = currColor == 1 ? 0 : 1;
}
return true;
}
}
Input
Output
#3 Code Example with Javascript Programming
Code -
Javascript Programming
const isBipartite = function (graph) {
const visited = Array(graph.length).fill(0);
for (let i = 0; i < graph.length; i++) {
if (visited[i] !== 0) {
continue;
}
const queue = [];
queue.push(i);
visited[i] = 1;
while (queue.length > 0) {
const index = queue.shift();
for (let j = 0; j < graph[index].length; j++) {
const temp = graph[index][j];
if (visited[temp] === 0) {
visited[temp] = visited[index] * -1;
queue.push(temp);
} else {
if (visited[temp] === visited[index]) return false;
}
}
}
}
return true;
};
Input
Output
#4 Code Example with Python Programming
Code -
Python Programming
class Solution:
def isBipartite(self, graph):
side = [0] * len(graph)
def dfs(node):
for v in graph[node]:
if side[v] == 0:
side[v] = -side[node]
if not dfs(v): return False
elif side[v] == side[node]: return False
return True
for i in range(len(graph)):
if side[i] == 0:
side[i] = 1
if not dfs(i): return False
return True
Input
Output
#5 Code Example with C# Programming
Code -
C# Programming
start coding...