Algorithm
Problem Name: 675. Cut Off Trees for Golf Event
Problem Link: https://leetcode.com/problems/cut-off-trees
forest = [[1,2,3],[0,0,0],[7,6,5]]. The forest is represented as an
m x n matrix. In this matrix:0means the cell cannot be walked through.1represents an empty cell that can be walked through.- A number greater than
1represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes 1 (an empty cell).
Starting from the point (0, 0), return the minimum steps you need to walk to cut off all the trees. If you cannot cut off all the trees, return -1.
Note: The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
Example 1:
Input: forest = [[1,2,3],[0,0,4],[7,6,5]] Output: 6 Explanation: Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
Example 2:
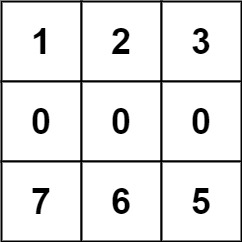
Input: forest = [[1,2,3],[0,0,0],[7,6,5]] Output: -1 Explanation: The trees in the bottom row cannot be accessed as the middle row is blocked.
Example 3:
Input: forest = [[2,3,4],[0,0,5],[8,7,6]] Output: 6 Explanation: You can follow the same path as Example 1 to cut off all the trees. Note that you can cut off the first tree at (0, 0) before making any steps.
Constraints:
m == forest.lengthn == forest[i].length1 <= m, n <= 500 <= forest[i][j] <= 109- Heights of all trees are distinct.
Code Examples
#1 Code Example with Java Programming
Code -
Java Programming
class Solution {
int[][] dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public int cutOffTree(List < List trees = new ArrayList<>();
for (int i = 0; i < forest.size(); i++) {
for (int j = 0; j < forest.get(i).size(); j++) {
if (forest.get(i).get(j) > 1) {
trees.add(new int[]{forest.get(i).get(j), i, j});
}
}
}
Collections.sort(trees, (a, b) -> Integer.compare(a[0], b[0]));
int totalDist = 0;
int startRow = 0;
int startCol = 0;
for (int[] tree : trees) {
int dist = getDistance(forest, startRow, startCol, tree[1], tree[2]);
if (dist < 0) {
return -1;
}
totalDist += dist;
startRow = tree[1];
startCol = tree[2];
}
return totalDist;
}
private int getDistance(List < List queue = new LinkedList<>();
queue.add(new int[]{startRow, startCol});
int[][] visited = new int[forest.size()][forest.get(0).size()];
visited[startRow][startCol] = 1;
while(!queue.isEmpty()){
int queueSize = queue.size();
steps++;
while(queueSize-- > 0) {
int[] cur = queue.poll();
int currRow = cur[0];
int currCol = cur[1];
for(int k = 0; k < 4; k++) {
int x = currRow + dir[k][0];
int y = currCol + dir[k][1];
if(x >= 0 && x < forest.size(> && y >= 0 && y < forest.get(0).size() && forest.get(x).get(y) > 0 && visited[x][y] == 0) {
if(x == desRow && y == desCol) {
return steps;
}
visited[x][y] = 1;
queue.add(new int[]{x, y});
}
}
}
}
return -1;
}
}
Input
forest = [[1,2,3],[0,0,4],[7,6,5]]
Output
6
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const cutOffTree = function (forest) {
const n = forest.length
if (n === 0) return 0
const m = forest[0].length
if (m === 0) return 0
const entries = []
for (let i = 0; i < n; i += 1) {
for (let j = 0; j < m; j += 1) {
if (forest[i][j] > 0) {
entries.push([forest[i][j], i, j])
}
}
}
entries.sort((e1, e2) => e1[0] - e2[0])
const direct = [
[1, 0],
[-1, 0],
[0, 1],
[0, -1],
]
const visited = Array(n)
.fill(null)
.map(() => Array(m).fill(0))
const bfs = function (start, end) {
for (let i = 0; i < n; i += 1)
for (let j = 0; j < m; j += 1) visited[i][j] = 0
let cur = [start],
next = [],
step = 0
visited[start[0]][start[1]] = 1
while (cur.length > 0) {
next = []
for (const [x, y] of cur) {
if (x === end[0] && y === end[1]) return step
for (const [dx, dy] of direct) {
const p = x + dx,
q = y + dy
if (
p < 0 ||
q < 0 ||
p >= n ||
q >= m ||
visited[p][q] === 1 ||
forest[p][q] === 0
)
continue
visited[p][q] = 1
next.push([p, q])
}
}
step += 1
cur = next
}
return -1
}
let pre = [0, 0],
totalCnt = 0
for (const entry of entries) {
const step = bfs(pre, entry.slice(1))
if (step === -1) return -1
totalCnt += step
pre = entry.slice(1)
}
return totalCnt
}
Input
forest = [[1,2,3],[0,0,4],[7,6,5]]
Output
6
#3 Code Example with Python Programming
Code -
Python Programming
class Solution:
def cutOffTree(self, forest):
def hadlocks(forest, sr, sc, tr, tc):
R, C = len(forest), len(forest[0])
processed = set()
deque = collections.deque([(0, sr, sc)])
while deque:
detours, r, c = deque.popleft()
if (r, c) not in processed:
processed.add((r, c))
if r == tr and c == tc:
return abs(sr-tr) + abs(sc-tc) + 2*detours
for nr, nc, closer in ((r-1, c, r > tr), (r+1, c, r < tr),
(r, c-1, c > tc), (r, c+1, c < tc)):
if 0 <= nr < R and 0 <= nc < C and forest[nr][nc]:
if closer:
deque.appendleft((detours, nr, nc))
else:
deque.append((detours+1, nr, nc))
return -1
trees = sorted((v, r, c) for r, row in enumerate(forest)
for c, v in enumerate(row) if v > 1)
sr = sc = ans = 0
for _, tr, tc in trees:
d = hadlocks(forest, sr, sc, tr, tc)
if d < 0: return -1
ans += d
sr, sc = tr, tc
return ans
Input
forest = [[1,2,3],[0,0,0],[7,6,5]]
Output
-1