Algorithm
Problem Name: 885. Spiral Matrix III
You start at the cell (rStart, cStart) of an rows x cols grid facing east. The northwest corner is at the first row and column in the grid, and the southeast corner is at the last row and column.
You will walk in a clockwise spiral shape to visit every position in this grid. Whenever you move outside the grid's boundary, we continue our walk outside the grid (but may return to the grid boundary later.). Eventually, we reach all rows * cols spaces of the grid.
Return an array of coordinates representing the positions of the grid in the order you visited them.
Example 1:
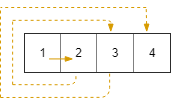
Input: rows = 1, cols = 4, rStart = 0, cStart = 0 Output: [[0,0],[0,1],[0,2],[0,3]]
Example 2:
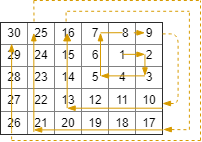
Input: rows = 5, cols = 6, rStart = 1, cStart = 4 Output: [[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]
Constraints:
1 <= rows, cols <= 1000 <= rStart < rows0 <= cStart < cols
Code Examples
#1 Code Example with Python Programming
Code -
Python Programming
class Solution:
def spiralMatrixIII(self, R, C, r0, c0):
direct, res, n, l, ind = [(-1, 0), (0, 1), (1, 0), (0, -1)], [[r0, c0]], R * C, 1, 1
while len(res) < n:
for __ in range(2):
for _ in range(l):
r0 += direct[ind][0]
c0 += direct[ind][1]
if 0 <= r0 < R and 0 <= c0 < C:
res.append([r0, c0])
ind = (ind + 1) % 4
l += 1
return res
Input
Output
#2 Code Example with C# Programming
Code -
C# Programming
namespace LeetCode
{
public class _0885_SpiralMatrixIII
{
public int[][] SpiralMatrixIII(int R, int C, int r0, int c0)
{
int[] dr = new int[] { 0, 1, 0, -1 };
int[] dc = new int[] { 1, 0, -1, 0 };
int[][] result = new int[R * C][];
int index = 0, direction = 0, step = 2;
result[index++] = new int[] { r0, c0 };
while (index < R * C)
{
var distance = step / 2;
for (int i = 0; i < distance; i++)
{
r0 += dr[direction];
c0 += dc[direction];
if (r0 >= 0 && r0 < R && c0 >= 0 && c0 < C)
{
result[index++] = new int[] { r0, c0 };
if (index == R * C) break;
}
}
direction++;
direction %= 4;
step++;
}
return result;
}
}
}
Input
Output
