Algorithm
Problem Name: 576. Out of Boundary Paths
There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.
Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo 109 + 7.
Example 1:
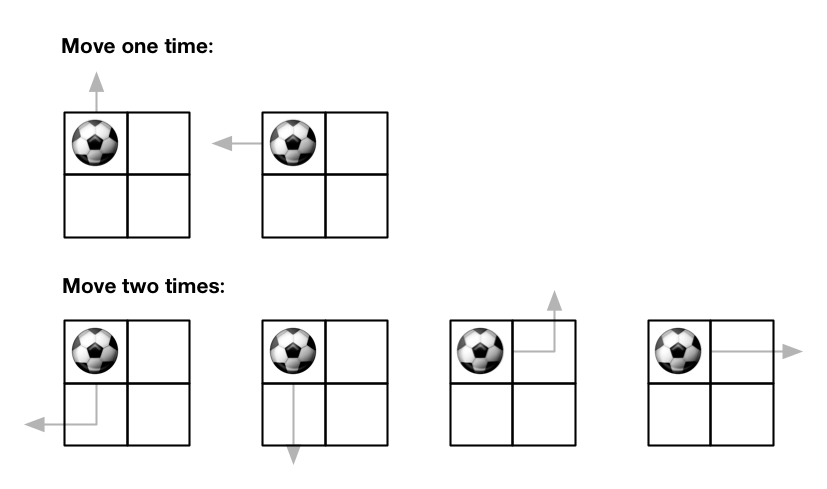
Input: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0 Output: 6
Example 2:
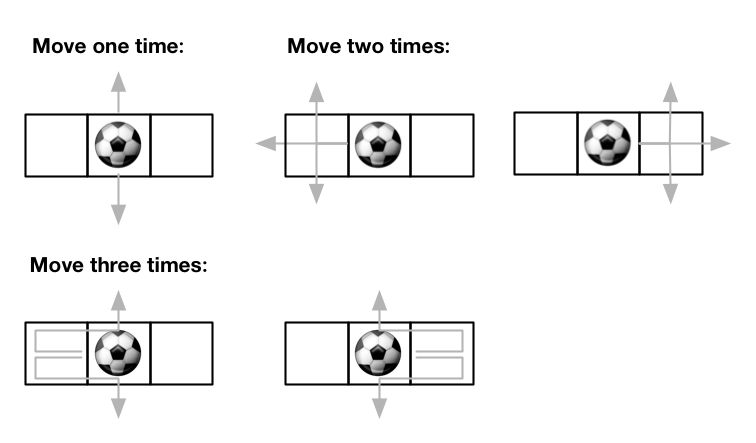
Input: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1 Output: 12
Constraints:
1 <= m, n <= 500 <= maxMove <= 500 <= startRow < m0 <= startColumn < n
Code Examples
#1 Code Example with Java Programming
Code -
Java Programming
class Solution {
private final int MODULUS = 1000000000 + 7;
public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
int dp[][] = new int[m][n];
dp[startRow][startColumn] = 1;
int count = 0;
for (int currMove = 1; currMove < = maxMove; currMove++) {
int[][] temp = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == m - 1) {
count = (count + dp[i][j]) % MODULUS;
}
if (j == n - 1) {
count = (count + dp[i][j]) % MODULUS;
}
if (i == 0) {
count = (count + dp[i][j]) % MODULUS;
}
if (j == 0) {
count = (count + dp[i][j]) % MODULUS;
}
temp[i][j] = (
((i > 0 ? dp[i - 1][j] : 0) + (i < m - 1 ? dp[i + 1][j] : 0)) % MODULUS +
((j > 0 ? dp[i][j - 1] : 0) + (j < n - 1 ? dp[i][j + 1] : 0)) % MODULUS
) % MODULUS;
}
}
dp = temp;
}
return count;
}
}
Input
Output
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const findPaths = function (m, n, N, i, j) {
const dp = [...Array(2)].map((_) =>
[...Array(50)].map((_) => Array(50).fill(0))
)
while (N-- > 0) {
for (let i = 0; i < m; i++) {
for (let j = 0, nc = (N + 1) % 2, np = N % 2; j < n; j++) {
dp[nc][i][j] =
((i === 0 ? 1 : dp[np][i - 1][j]) +
(i === m - 1 ? 1 : dp[np][i + 1][j]) +
(j === 0 ? 1 : dp[np][i][j - 1]) +
(j === n - 1 ? 1 : dp[np][i][j + 1])) %
1000000007
}
}
}
return dp[1][i][j]
}
Input
Output
#3 Code Example with Python Programming
Code -
Python Programming
class Solution:
def __init__(self): self.dic = collections.defaultdict(int)
def findPaths(self, m, n, N, i, j):
if N >= 0 and (i < 0 or j < 0 or i >= m or j >= n): return 1
elif N < 0: return 0
elif (i, j, N) not in self.dic:
for p in ((1, 0), (-1, 0), (0, 1), (0, -1)): self.dic[(i, j, N)] += self.findPaths(m, n, N - 1, i + p[0], j + p[1])
return self.dic[(i, j, N)] % (10 ** 9 + 7)
Input
Output
