Algorithm
Problem Name: 986. Interval List Intersections
You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.
Return the intersection of these two interval lists.
A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.
The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].
Example 1:
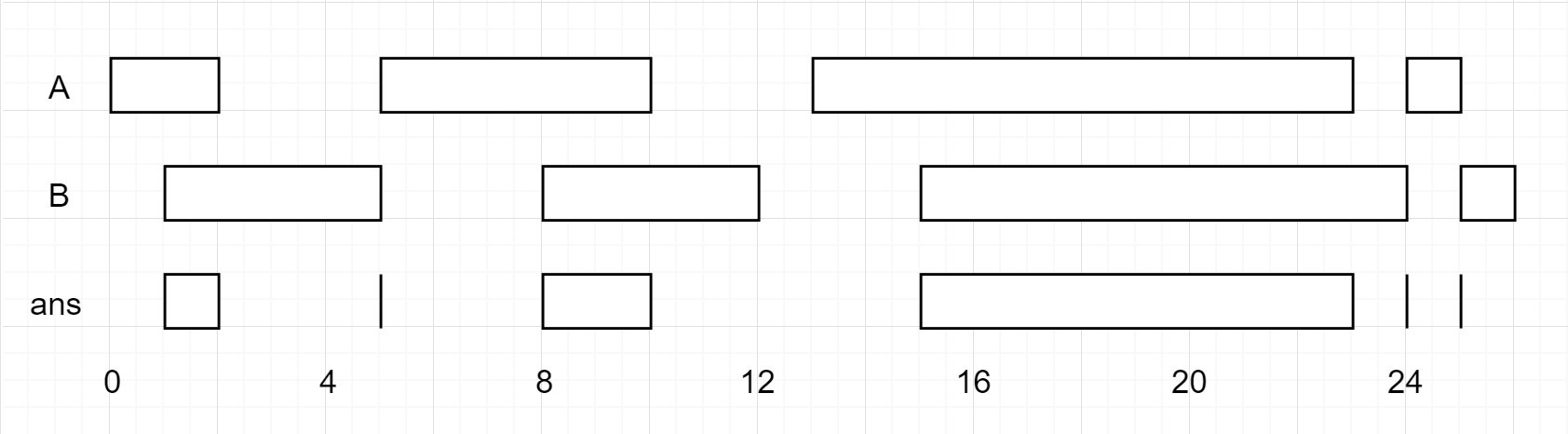
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]] Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Example 2:
Input: firstList = [[1,3],[5,9]], secondList = [] Output: []
Constraints:
0 <= firstList.length, secondList.length <= 1000firstList.length + secondList.length >= 10 <= starti < endi <= 109endi < starti+10 <= startj < endj <= 109endj < startj+1
Code Examples
#1 Code Example with C Programming
Code -
C Programming
typedef struct {
int **p;
int *c;
int n;
int sz;
} res_t;
void add2res(res_t *res, int x, int y) {
int *buff = malloc(2 * sizeof(int));
//assert(buff);
buff[0] = x; buff[1] = y;
if (res->sz == res->n) {
if (res->sz == 0) res->sz = 10;
else res->sz *= 2;
res->p = realloc(res->p, res->sz * sizeof(int *));
res->c = realloc(res->c, res->sz * sizeof(int));
//assert(res->p);
}
res->p[res->n] = buff;
res->c[res->n ++] = 2;
}
int _min(int a, int b) {
if (a < b) return a;
return b;
}
int _max(int a, int b) {
if (a > b) return a;
return b;
}
int** intervalIntersection(int** A, int ASize, int* AColSize, int** B, int BSize, int* BColSize, int* returnSize, int** returnColumnSizes){
res_t res = { 0 };
int i, j, x, y;
int *a, *b;
i = 0, j = 0;
while (i < ASize && j < BSize) {
a = A[i]; b = B[j];
x = _max(a[0], b[0]);
y = _min(a[1], b[1]);
if (x < = y) add2res(&res, x, y);
if (a[1] > b[1]) j ++;
else i ++;
}
*returnColumnSizes = res.c;
*returnSize = res.n;
return res.p;
}
Input
Output
#2 Code Example with Java Programming
Code -
Java Programming
class Solution {
public int[][] intervalIntersection(int[][] firstList, int[][] secondList) {
List<int[]> list = new ArrayList<>();
int idxOne = 0;
int idxTwo = 0;
while (idxOne < firstList.length && idxTwo < secondList.length) {
int maxStart = Math.max(firstList[idxOne][0], secondList[idxTwo][0]);
int minEnd = Math.min(firstList[idxOne][1], secondList[idxTwo][1]);
if (maxStart < = minEnd) {
list.add(new int[]{maxStart, minEnd});
}
if (minEnd == firstList[idxOne][1]) {
idxOne++;
} else {
idxTwo++;
}
}
int[][] result = new int[list.size()][2];
return list.toArray(result);
}
}
Input
Output
#3 Code Example with Javascript Programming
Code -
Javascript Programming
const intervalIntersection = function (A, B) {
const intersection = []
let i = (j = 0)
while (i < A.length && j < B.length) {
const min = Math.max(A[i][0], B[j][0])
const max = Math.min(A[i][1], B[j][1])
if (min <= max) intersection.push([min, max])
A[i][1] > B[j][1] ? j++ : i++
}
return intersection
}
Input
Output
#4 Code Example with Python Programming
Code -
Python Programming
class Solution:
def intervalIntersection(self, A: List[Interval], B: List[Interval]) -> List[Interval]:
i = j = 0
res = []
while i < len(A) and j < len(B):
s = max(A[i].start, B[j].start)
e = min(A[i].end, B[j].end)
if s <= e:
res.append(Interval(s, e))
if A[i].end < B[j].end:
i += 1
elif A[i].end == B[j].end:
i += 1
j += 1
else:
j += 1
return res
Input
Output
#5 Code Example with C# Programming
Code -
C# Programming
using System;
using System.Collections.Generic;
namespace LeetCode
{
public class _0986_IntervalListIntersections
{
public int[][] IntervalIntersection(int[][] A, int[][] B)
{
var result = new List < int[]>();
int i = 0, j = 0;
while (i < A.Length && j < B.Length)
{
var lo = Math.Max(A[i][0], B[j][0]);
var hi = Math.Min(A[i][1], B[j][1]);
if (lo < = hi)
result.Add(new int[] { lo, hi });
if (A[i][1] < B[j][1])
i++;
else
j++;
}
return result.ToArray();
}
}
}
Input
Output
