Algorithm
Problem Name: 861. Score After Flipping Matrix
You are given an m x n binary matrix grid.
A move consists of choosing any row or column and toggling each value in that row or column (i.e., changing all 0's to 1's, and all 1's to 0's).
Every row of the matrix is interpreted as a binary number, and the score of the matrix is the sum of these numbers.
Return the highest possible score after making any number of moves (including zero moves).
Example 1:
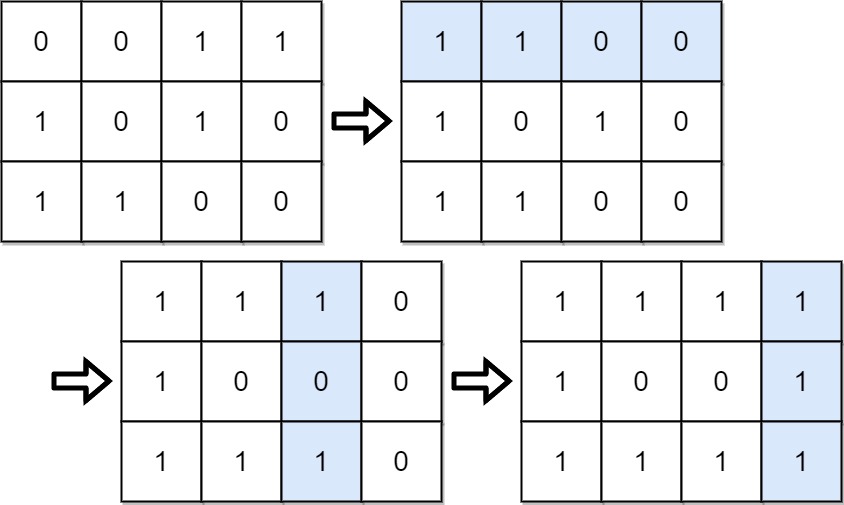
Input: grid = [[0,0,1,1],[1,0,1,0],[1,1,0,0]] Output: 39 Explanation: 0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39
Example 2:
Input: grid = [[0]] Output: 1
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 20grid[i][j]is either0or1.
Code Examples
#1 Code Example with Java Programming
Code -
Java Programming
class Solution {
public int matrixScore(int[][] A) {
for (int i=0; i < A.length; i++) {
int actualSum = getDecimalValue(A[i], false);
int toggledSum = getDecimalValue(A[i], true);
if (toggledSum > actualSum) {
for (int j=0; j < A[i].length; j++) {
A[i][j] ^= 1;
}
}
}
for (int i=0; i < A[0].length; i++) {
int numZeroes = 0;
int numOnes = 0;
for (int j=0; j < A.length; j++) {
if (A[j][i] == 1 ) {
numOnes++;
}
else {
numZeroes++;
}
}
if (numZeroes > numOnes) {
for (int j=0; j < A.length; j++) {
A[j][i] ^= 1;
}
}
}
int maxSum = 0;
for (int[] arr : A) {
maxSum += getDecimalValue(arr, false);
}
return maxSum;
}
private int getDecimalValue(int[] arr, boolean isToggled) {
int sum = 0;
int pow = 0;
for (int i=arr.length-1; i>=0; i--) {
if (isToggled) {
sum += Math.pow(2, pow) * (arr[i] ^ 1);
}
else {
sum += Math.pow(2, pow) * arr[i];
}
pow++;
}
return sum;
}
}
Input
Output
#2 Code Example with Javascript Programming
Code -
Javascript Programming
const matrixScore = function(grid) {
const m = grid.length, n = grid[0].length
let res = 0
res += m * (1 << (n - 1))
for(let j = 1; j < n; j++) {
let same = 0
for(let i = 0; i < m; i++) {
if(grid[i][0] === grid[i][j]) same++
}
res += Math.max(same, m - same) * (1 << (n - 1 - j))
}
return res
};
Input
Output
#3 Code Example with Python Programming
Code -
Python Programming
class Solution:
def matrixScore(self, A):
for i, row in enumerate(A):
if not row[0]:
A[i] = [1 - num for num in row]
m, n, sm = len(A), len(A and A[0]), 0
for c in range(n):
cnt = sum(A[r][c] for r in range(m))
sm += max(cnt, m - cnt) * 2 ** (n - c - 1)
return sm
Input
Output
#4 Code Example with C# Programming
Code -
C# Programming
using System;
namespace LeetCode
{
public class _0861_ScoreAfterFlippingMatrix
{
public int MatrixScore(int[][] A)
{
var rows = A.Length;
var cols = A[0].Length;
var result = 0;
for (int c = 0; c < cols; c++)
{
var colsum = 0;
for (int r = 0; r < rows; r++)
colsum += A[r][c] ^ A[r][0];
result += Math.Max(colsum, rows - colsum) * (int)Math.Pow(2, cols - c - 1);
}
return result;
}
}
}
Input
Output
